November 19, 2025
In longitudinal data with irregularly timed visits, semi-parametric joint models have been proposed to account for the dependence between times and the Sun model (Sun et al, 2011) has been the most suitable for count data. The authors have extended the Sun model to additionally estimate the intercept term through a parametric functional form. The Sun model used a multiplicative model for the longitudinal outcome. They modeled the intercept which is in their intensity model and for the Bt(t) function, they used a spline basis function for flexibility. They used this in the estimation of their process and likelihood. For variance estimation they used bootstrap sampling. They also defined some diagnostics for goodness-of-fit of the marginal regression model by defining a residual function which is similar to Sun et al (2011) which uses a Breslow estimator of the integrated baseline hazard.
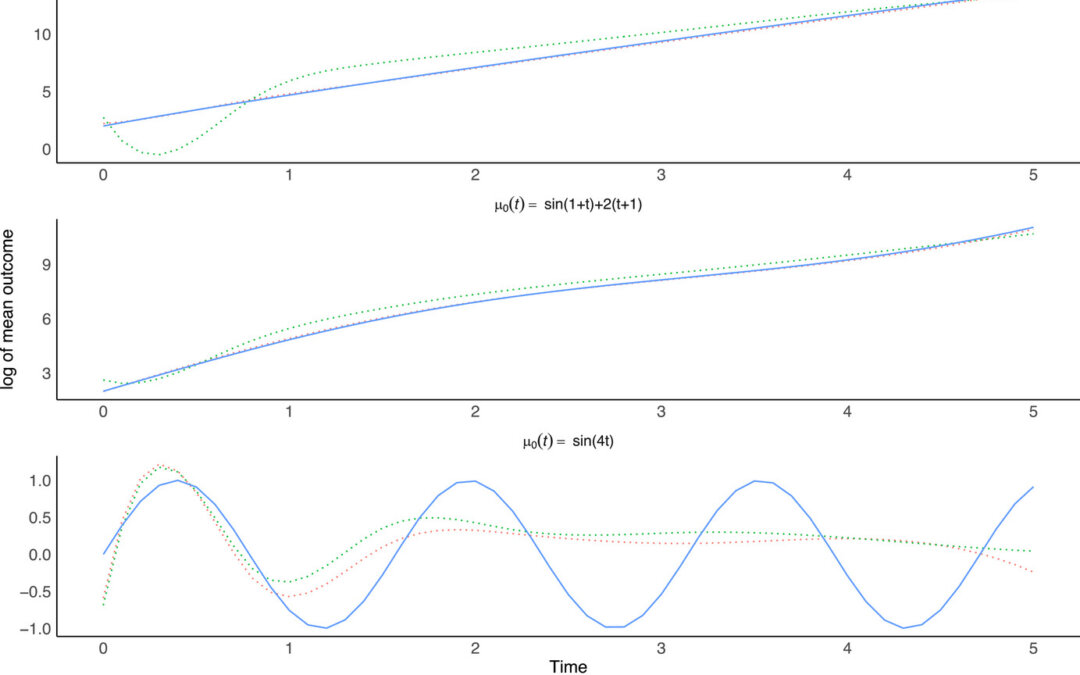
They conducted a simulation study to assess how the estimator varied across different functional forms for the intercept by analyzing the bias and empirical standard error (ESE) decreases. They found that the extended Sun model resulted in a lower bias of the relative effects compared to the other estimation techniques and also this bias decreased as sample size increased as well as the ESE (see Table 2). For the different values of tau, they found that the extended Sun model had a lower ESE than the regular Sun model. The extended Sun model also maintained a smaller bias than the original Sun and GEE models when the intercept was varied. For the extended Sun model, they found that the ESE estimates did not appear to greatly change across the different variations of the intercept. For the first two variations of the intercept term (log-linear and sine-linear), their new model estimated the outcome trajectory with less bias than the GEE with splines (Figure 1). However, for the sinusoidal intercept, neither model was able to recover the true mean outcome trajectory.
In their real dataset analysis, they used a frailty term in the Cox model around the visit process and a cubic B-spline with 3 knots. They compared their extended Sun model to a GEE spline model and the Sun model. Overall their model did well. Overall, as the authors have said, their proposed estimation procedure allows for the estimation of the outcome trajectory for an outcome measured irregularly over time with observation times linked to the outcome via observed baseline covariates and a random effect.
Written by,
Usha Govindarajulu
Keywords: semi-parametric, joint models, longitudinal, irregularly timed observations
References:
Ledesma L and Pullenayegum E (2025) “Intercept Estimation of Semi-Parametric Joint Models in the Context of Longitudinal Data Subject to Irregular Observations” Biometrical Journal. https://doi.org/10.1002/bimj.70088.
Sun, L., X.-Y. Mu, Z.-H. Sun, and X.-W. Tong. 2011. “Semiparametric Analysis of Longitudinal Data With Informative Observation Times.” Acta Mathematicae Applicatae Sinica, English Series 27, no. 1: 29–42.
https://onlinelibrary.wiley.com/cms/asset/c16885bc-f3c0-45f1-a501-fac9c09067d6/bimj70088-fig-0001-m.jpg