September 10, 2025
The authors developed a general estimation method for inference in partially linear models with nonmonotone missing at random data. The unified estimation method was already developed for parametric regression models with nonmonotone MAR data where it extracts partial information from the incomplete observations to improve estimation efficiency of the complete data method. It is consistent regardless of the correctness of the working models as long as the missing data probabilities are known or can be estimated. They counted the total number of distinct missingness patterns by variables being observed and missing together being in the same missing data pattern.
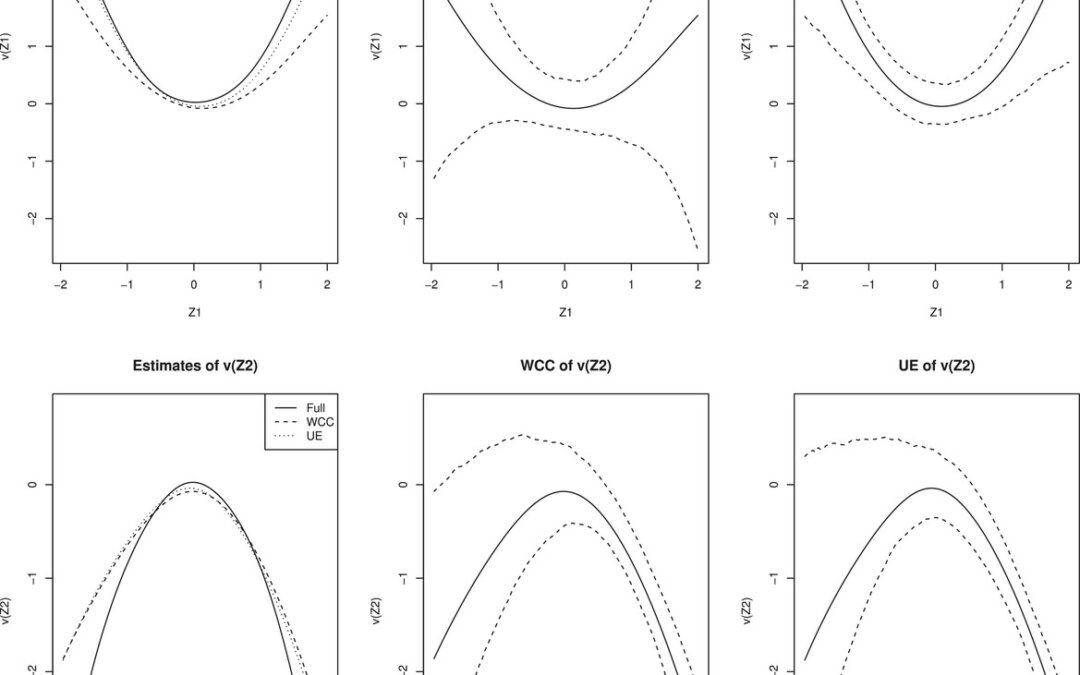
Partially linear models had been estimated by the weighted complete case method (WCC) which uses inverse probability weighted estimating equation. Though easy to commute it had not been efficient since it ignores information in the incomplete observations. In their unified approach (UE), they if the estimated missing probabilities are known than the unified parameter estimate of beta is more efficient than the WC estimate of beta. The estimated of variance-covariance matrices can be computed using the analytic sandwich estimator. The missing data probabilities are estimated from semiparametric or nonparametric models. For sparsely observed missingness patterns, they chose semiparametric models for the missing data probabilities which required using an expectation-maximization algorithm (EM) to compute these estimates. An alternative to this is to use the bootstrap method to estimate the variance-covariance matrices. Through simulations on the WC, improved WC estimate, and the UE for Cox proportional hazards models, they found the bootstrap estimates were very similar to the estimates from the sandwich estimator. The UE is a linear function of the standard WC estimators and its asymptotic properties depend on the WCC estimators. They were able to also extend their method to estimate the missing data probabilities using both the fully observed and partially observed variables.
They ran simulations and found the UE method was in general better than the WCC estimate. In a real dataset analysis, they estimated missing data probabilities using logistic regression models and for sparsely observed patterns they used the semiparametric maximum likelihood estimation method where empirical distributions for missing covariates are treated as nuisance parameters and an EM algorithm with closed-form expressions for both the E-step and the M-step are used to compute the estimate. For this real dataset analysis, the UE was slightly more efficient than the WCC estimate. At no point do the authors really discuss the missing data patterns, especially the non-monotone patterns of which they had included in the title in the first place. Secondly, they used Cox proportional hazards regression models to generate missing probabilities but they did not discuss the ramifications of the proportional hazards assumption. Their methods are not explained well for generating these missing probabilities.
Written by,
Usha Govindarajulu
Keywords: partially linear models, nonmonotone. missing at random, Cox models, EM algorithm, non-parametric
References:
Zhao, Y. (2025) “Unified Estimation Method for Partially Linear Models With Nonmonotone Missing at Random Data” Biometrical Journal. https://doi.org/10.1002/bimj.70070
https://onlinelibrary.wiley.com/cms/asset/2a1e0889-08c3-4258-8c05-bd4b7b1ba3b3/bimj70070-fig-0001-m.jpg