April 12, 2023
The authors, Ozaki and Ninomiya have presented how information criteria, like AIC, can be adapted when detecting change points in a Cox proportional hazards regression. The authors motivated the use of change-points due to onset of efficacy being delayed in clinical trials comparing various therapeutics. They also motivated this for the case where proportional hazards does not hold due to these types of trials.
In terms of their methods development, the authors took the partial likelihood and induced a regularized log-partial likelihood function with a ridge-type regularization term. They then expanded using the regularized log-partial likelihood function in their adapted AIC for change-points, which can easily default back to the general AIC when there are no change-points. Usually in the AIC calculation there is 2 multiplied by number of parameters, but this has changed with their method. According to their derivations, the asymptotic bias due to the change-point parameter is three times greater than that due to the regression parameter and they then propose a new AIC criterion in their equation (20), to which they refer to as the AIC for the Cox model with change-points, for estimation which was based on the conventional partial likelihood method.
They then conducted numerical experiment to test to the performance of this AIC proposed criterion to the following that use the usually way of handling bias due to regression parameters but now for the change-point parameter. In Table 2, they reported the Kullback-Leibler divergence between true and estimated distributions along with the selection probabilities. They found their AIC would in general produce a smaller Kullback-Leibler divergence score than the regular AIC under any setting of no or multiple change-points. They also additionally compared it to a BIC and still found their AIC performed better.
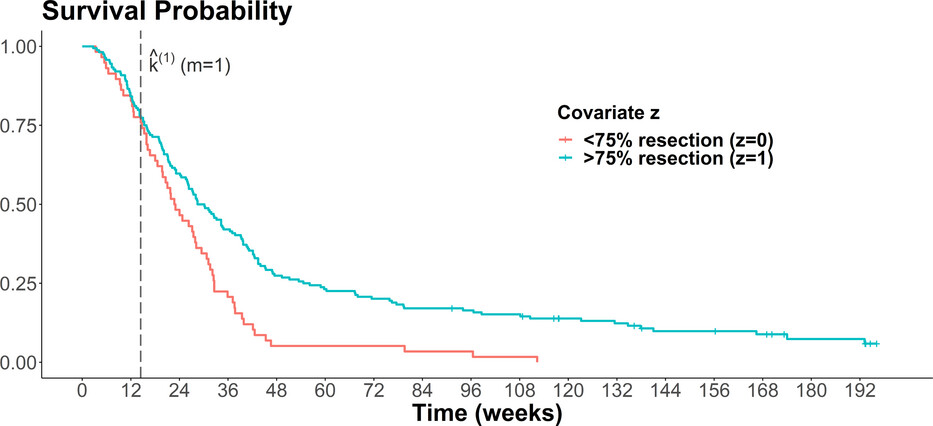
Finally they applied their AIC method to a real dataset from a randomized, placebo-controlled trial of patients with malignant glioma at multiple sites. Therefore, to check a model with change-points, they tried out anymore from none to 4 change-points and tested their goodness of fit through the AIC method compared to regular AIC and BIC. The three information criterion were divergent where their AIC selected a model with 4 change-points, regular AIC selected a model with 1 change-point, and BIC selected a model with none. They further also considered model misspecification and did some simulations under this scenario.
Although the authors have seem to have obtained success in their method through numerical simulations, it was not clear that this method will work well in real data examples, which then they tried to explain in their discussion that they were able to show outside of that that even with model misspecification that their method could work. However, through a careful read of this article, this type of modeling does not at this time appear completely robust and as they mentioned, the divergence of proportional hazards and the differences in speed of Brownian motion of processes can make it difficult to capture change-points.
Written by,
Usha Govindarajulu
Keywords: survival, Cox model, change point, AIC, information criteria
References
Ozaki R and Ninomiya Y (2023). “Information criteria for detecting change-point in the Cox proportional hazards model” Biometrics. https://doi.org/10.1111/biom.13855
https://onlinelibrary.wiley.com/cms/asset/fa24f218-c8ce-4104-9697-683651801085/biom13855-fig-0001-m.jpg