June 7, 2023
The authors reviewed methods for complex survival data in terms of frailty models, like the recent advances and R packages. They explored areas of clustered outcomes, competing risks, illness-death model. They did admit their review did not cover two popular methods for clustered data: marginal Cox or AFT regression methods nor copula models. It was hard to understand why they would leave out these popular methods. Throughout the manuscript, they provided certain referebces when so much work exists for many of these methods, namely the background and theory and then lead to their references, like a pseudolikelihood procedure for which they try to show the superiority of their method.
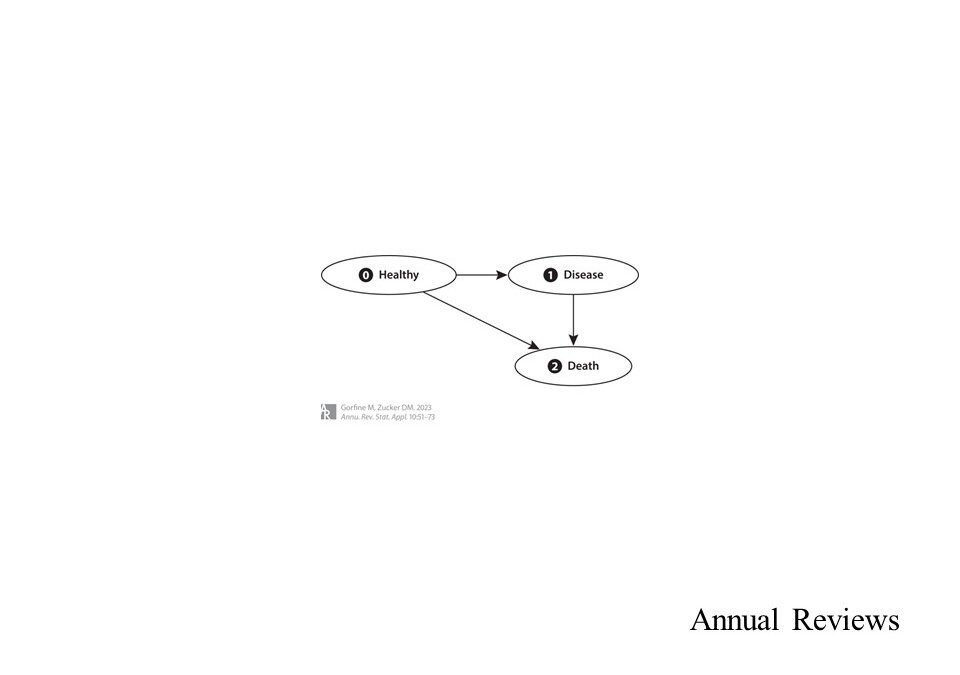
They then discussed AFT frailty models. They focused a lot on a paper by Lambert (2004). They then discussed estimation of clustered AFT models and also an R software package. Finally they get into Cox models with clustering and competing risks. In this section, they discussed their paper quite a bit, Gorfine & Hsu (2011), and their semi-parametric estimation method for this type of model. Next they dwelved into semi-parametric illness-death models, where there are multiple states or transitions. Again after discussing some of the literature, they again got into their method in which they used frailty in a Cox model with marginal hazards. Apparenthly, AFT methods are better developed in this area. The second to last section was recurrent events. In this section, they brought up the counting process version of the Cox model, especially because a Cox process, similar to a Poisson process, was introduced to handle this issue. Finally they introduced frailty models for this context. However, a model they introduced from Bender et al (2018) used a piecewise-exponential additive mixed effects model.
Finally there last section discussed random survival forests for clustered data. They largely discussed the theory behind the random survival forests (RSF). They then discussed the RSF combined with frailty in newer methods, where at each node a Cox model incorporating frailty was estimated, i.e. based on a penalized partial likelihood approach (Therneau, 2003)/ or even a maximized integrated log-likelihood at each note. The authors mentioned these approaches had problems and failed to converge in large datasets. Newer approaches then were sought and the development in this area continues.
In their conclusions, the authors noted several areas still open to research. One was semi-parametric AFT models for clustered data and a single outcome with various frailty distributions other than gamma. The second was frailty-based AFT models for clustered data with competing events. The third is semicompeting risks via illness-death AFT models with other frailty distributions besides gamma. They also mentioned there could be a need for clusterd random survival forests. A final mention of clustered data with informative censoring or clustered data in cure models. Once again they reference their articles for future reference. A large area that was missing from this article is copula models, which they did mention in the beginning and they also never got into any detail about cure models. Mostly this “overview’ while there of select research was largely geared towards the authors’ own research and how that fit into the areas they mentioned, except for the random survival forests.
Written by,
Usha Govindarajulu
Keywords: survival, frailty, competing risks, recurrent events, illness-death, clustering, random survival forests
References
Bender A, Groll A, Scheipl F. 2018. A generalized additive model approach to time-to-event analysis. Stat. Model. 18(3/4):299–321.
Gorfine M, Hsu L. 2011. Frailty-based competing risks model for multivariate survival data. Biometrics 67(2):415–26.
Gorfine M and Zucker DM (2023) “Shared Frailty Methods for Complex Survival Data: A Review of Recent Advances” Annual Review of Statistics and Its Application. 10(1): 51-73.
https://www.annualreviews.org/doi/abs/10.1146/annurev-statistics-032921-021310
Lambert P, Collett D, Kimber A, Johnson R. 2004. Parametric accelerated failure time models with random effects and an application to kidney transplant survival. Stat. Med. 23(20):3177–92.
Therneau TM, Grambsch PM, Pankratz VS. 2003. Penalized survival models and frailty. J. Comput. Graph. Stat. 12(1):156–75.
https://www.annualreviews.org/na101/home/literatum/publisher/ar/journals/content/statistics/2023/statistics.2023.10.issue-1/annurev-statistics-032921-021310/20230220/images/medium/st10051.f1.gif