January 17, 2023
In an article that appeared in Biometrical Journal, Hoogland et al (2023) had aimed to combine the benefits of flexible parametric survival modeling and regularization in order to improve risk prediction modeling in the context of time-to-event data. They wanted to do this to improve out of sample accuracy over time where sample size may be limited for model complexity. For regularization methods, they considered the elastic-net penalty and the group lasso.
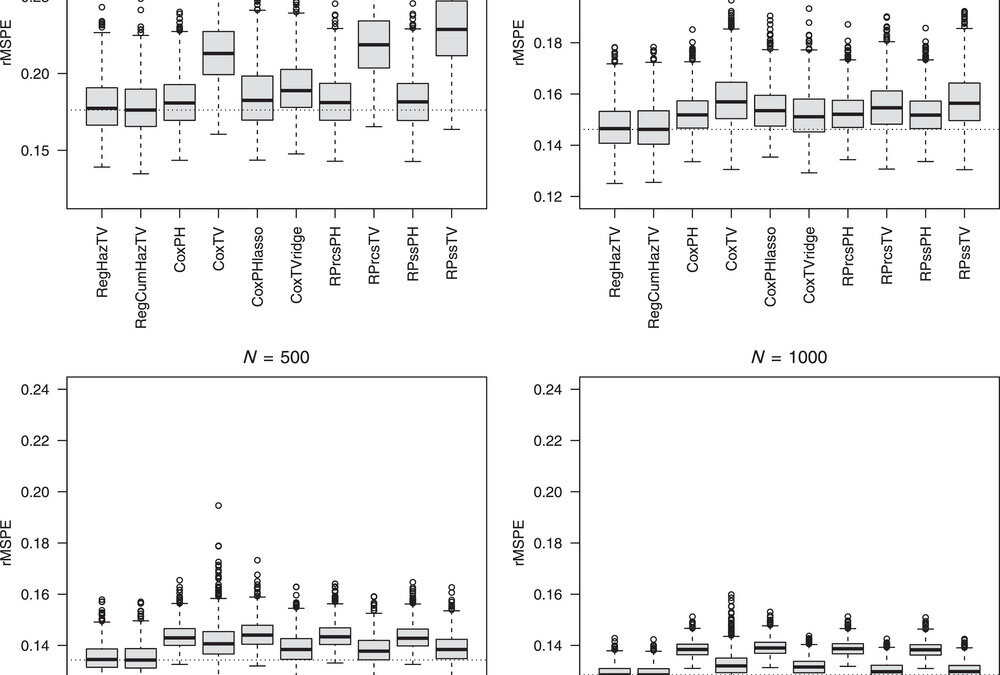
They conducted a simulation study with survival data generated from a two-component mixture model. They allowed for a non-monotone hazard function. They employed ten different modeling techniques to compare to their methods that ranged from regularized log hazard model with time-varying effects and/or with baseline hazard modeling by restricted cubic splines, Cox models that were basic or with time-varying effects or with lasso or ridge penalties on parameters, and Royston-Parmar proportional hazard models with natural cubic spline or smoothing spline for the baseline hazard and/or time-varying effects. In terms of measure of performance, they calculated a root mean squared prediction error for prediction accuracy at certain time points. They also evaluated fixed and time-average discriminative prediction performances against true survival probabilities by Harrell’s c-statistic. Calibration was assessed using graphical calibration curves at fixed time points.
In terms of results from the simulations, their regularized parametric methods performed well across all sample sizes. In terms of computational efficiency, the time-varying methods were overall slower. When they tested their methods and the other methods on a real dataset, they found that the c-statistics for their methods were somewhat lower than the other methods on time-averaged and higher on the 60-day followup. They implemented their methods in an R package, regsurv. Their package differs from other package in terms of modeling because theirs use fully parametric models whereas the others use Cox models. The authors did not elaborate too much on the fact that their method relies on fully parametric modeling and did not provide much regarding any limitations of their methods in their discussion section so .
Written by,
Usha Govindarajulu
Keywords: survival, regularization, flexible parametric, Royston-Parmar, Cox model, restricted cubic splines, time-varying, smoothing splines,
References
Hoogland J, Debray TPA, Crowther MJ, Riley RD, IntHout J, Reitsma JB, and Zwinderman AH
“Regularized parametric survival modeling to improve risk prediction models” Biometrical Journal.
https://doi.org/10.1002/bimj.202200319
https://onlinelibrary.wiley.com/cms/asset/5b337500-b89c-4b08-86ca-1238c5883bae/bimj2529-fig-0001-m.jpg