September 25, 2023
The authors, Hanke et al, discussed variable selction methods for linear regression and that the best subset selection (BSS) is not always the best choice. After Bertsimas et al (2016) pushed BSS as a mixed-integer optimization problem (MIO) so that number of optimal variables could be in the thousands then they were able to compare this method to variable selection methods like absoluate shrinkage and selection estimator (Lasso, Tibshirani, 1996), adaptive lasso (Zou, 2006) and elastic net (Zou & Hastie, 2005; Zou & Zhang, 2009). Hastie et al (2020) was first to do extensive study comparing BSS to Lasso and did not find one out-performing the other. He had focused on comparing predictive performance while they are focusing on ability to select correct direct predictors. They used the MIO formulation so BSS could be used in high-dimensional settings.
In their methods, the authors discussed a penalized least squares approach, a penalty term to thrink the estimated coefficients towards zero and also the BSS, also in the MIO reformulation. They also discussed forward stepwise selection (FSS) as a popular alternative to BSS, though the stepwise procedures have numerous drawbacks, as they point out. They said that the FSS can be interpreted as a greedy heurisitic vesion of BSS. They also discussed the Lasso (Tibshirani, 1996), which as they pointed out while it can do variable selection, it can come at a price in situations with high pairwise correlation between predictors. An alternative is the Enet (Zou & Hastie, 2005), which can be formulated as a weighted combination of the Lasso and an additional L2-penalization (Ridge) term. This second term was designed to help with highly correlated variables.
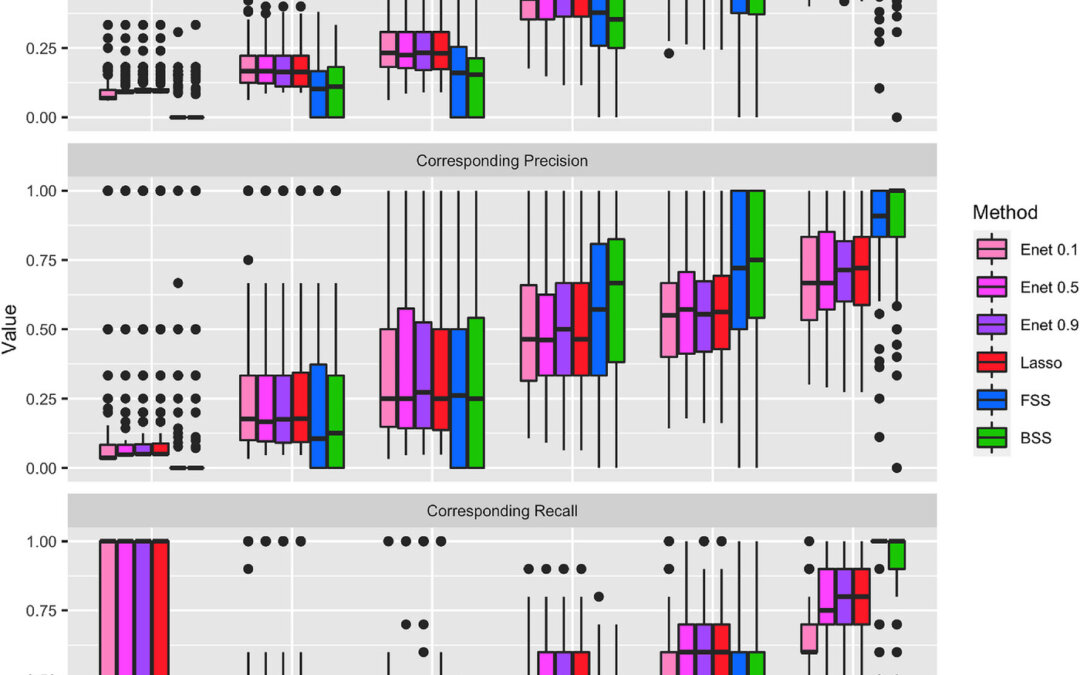
Hanke et al then tested the BSS, FSS, Lasso, and Enet in simulations. Also, the tuning parameter and also the set size had to be set a priori so the authors then had chosen a grid of parameters for each value. In addition, the BSS with MIO had to run with a set time limit. They found that the BSS outperformed the other methods in settings with high signal-to-noise ratio and when variables are uncorrelated, an unrealistic situation. As soon as variables started becoming correlated, the BSS performance dropped and even the Lasso, which has poor performance amongst correlated variables, performed better than the BSS in these situations. The FSS achieved similar performance as the BSS in almost all settings and did sometimes perform better. The BSS was inferior to the Lasso and the Enet in settings with low to moderate signal to noise ratio. They found similar results in semisynthetic data as well. However, they had not done a detailed assessment of selecting tuning parameters and subset size. Therefore, they concluded that in general, the Lasso and Enet outperformed the BSS and FSS.
Written by,
Usha Govindarajulu
Keywords: variable selection, linear regression models, subset, Lasso, Enet, best subset selection, forward stepwise selection, tuning parameter, MIO
References
Bertsimas, D., King, A., & Mazumder, R. (2016). Best subset selection via a modern optimization lens. Annals of Statistics, 44(2), 813–852.
Hanke M, Dijkstra L, Foraita R, and Didelez V (2023) “Variable selection in linear regression models: Choosing the best subset is not always the best choice”, Biometrical Journal, https://doi.org/10.1002/bimj.202200209
Hastie, T., Tibshirani, R., & Tibshirani, R. (2020). Best subset, forward stepwise or Lasso? Analysis and recommendations based on extensive comparisons. Statistical Science, 35(4), 579–592.
Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society, Series B, 58, 267–288.
Zou, H. (2006). The Adaptive Lasso and its oracle properties. Journal of the American Statistical Association, 101(476), 1418–1429.
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the Elastic Net. Journal of the Royal Statistical Society, Series B, 67, 301–320.
Zou, H., & Zhang, H. H. (2009). On the Adaptive Elastic-Net with a diverging number of parameters. Annals of Statistics, 37(4), 1733–1751.
https://onlinelibrary.wiley.com/cms/asset/365ab9a1-5c42-48ba-aab3-9de9299a8a8f/bimj2515-fig-0002-m.jpg