June 5, 2024
The authors have come up with a proportional risk model to assess treatment effect in time-to-event data. One thing they first discussed which is important to note is that relative risk (RR) and hazard ratio (HR) are definitely not the same measures since the hazard ratio is based on instantaneous rates and the RR is not. Also, the authors did mention that sometimes people confuse the odds ratio with the RR which is also not acceptable. Also, they brought up the proportional hazard assumption and how difficult this assumption can be and that the proportional odds (PO) assumption is also not always suitable. Therefore, a proportional risk model for a two group situation in RCTs was developed and the authors then based their idea on this.
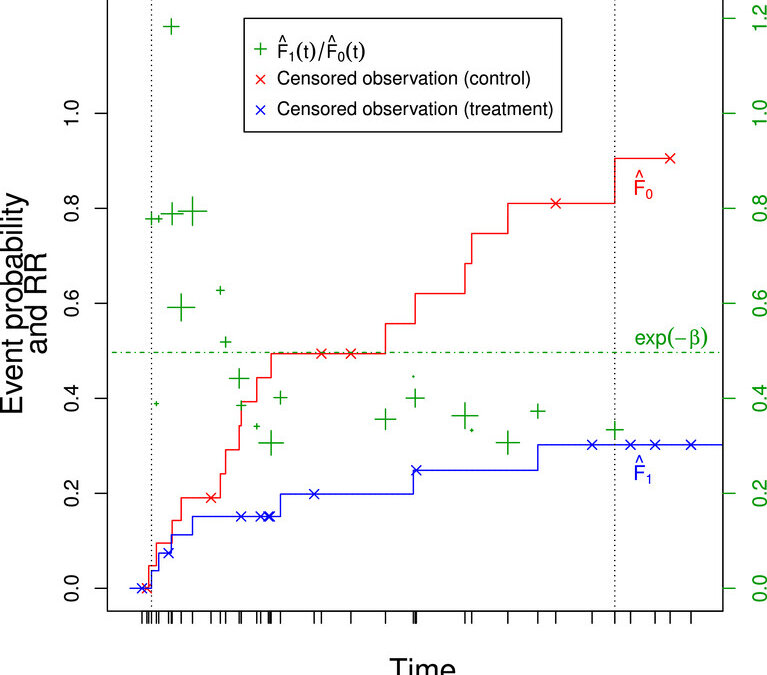
The authors then defined their nonparametric proportional risk estimator (NPPR) for the RR which would be easy to interpret. Their NPPR estimate derived has inverse weights which are based on variance of the estimated betas. After this they derived a risk difference between the unknown true CDFs. A Kaplan-Meier estimate is used for the control group CDF. The NNT is defined as the reciprocal of the risk difference. They then evaluated their NPPR estimator in simulations compared to the usual HR from a Cox model and the log-logistic PO model. The NPPR estimator performed well when compared in terms of MSE, coverage, and robustness.
In their discussion, they did discuss the limitations like that the NPPR contains only one binary variable and it was not possible to include further variables in the model. Also, having continuous variables was a problem. Given these discussions, it would seem the NPPR has limited usefulness in practice. It is like a replacement for the Kaplan-Meier with an average RR interpretation.
Written by,
Usha Govindarajulu, PhD
Keywords: survival analysis, hazard ratio, non-proportional hazards, risk ratio, proportional odds
References
Ameis L, Kuss O, Hoyer A, and Mollenhoff K (2024) “A nonparametric proportional risk model to assess a treatment effect in time-to-event data” Biometrics, 66(4): 2300147.
https://doi.org/10.1002/bimj.202300147
https://onlinelibrary.wiley.com/cms/asset/5feca0dd-16dd-46f8-a255-35d65d2839fd/bimj2579-fig-0001-m.jpg