January 3, 2022
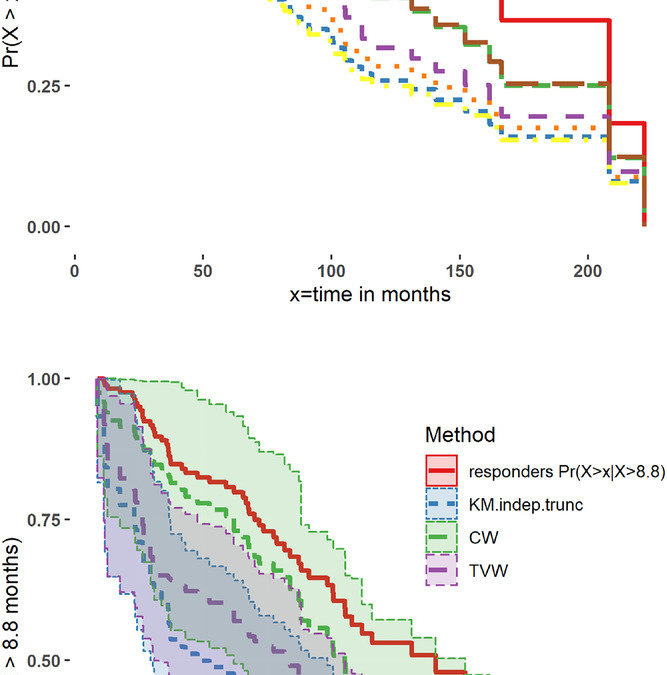
In an article originally published online August 13, 2021, but published recently in print, Vakulenko-Lagun et al discuss a technique to handle dependence between event times and left truncation. The left truncation generally happens due when there is delayed entry into an observational study. Though other methodologies have before been presented in the past by different authors, Vakulenko-Lagun et al proposed using two inverse probability-weighted estimators for the survival function that would allow accounting for dependence induced by covariates via modeling of the truncation distribution conditional on covariates.
In the development of their theory, the authors assumed there were no ties in the data. This would be an important point as many survival datasets have tied event times. Their description about their weighted estimators of SCW(x)-hat and STVW(x)-hat, mainly how they are derived, have not been easy to follow in their description in their methods. Their description about the weights and how they are obtained seemed mostly reasonable. In each theoretical section in the Methods, they seem to rely often on already proven theory and it would appear they were sometimes just subtly extending those theories, especially upon that developed by Jamie Robbins and others through causal inference. Their development of the propensity score for truncation is not straightforward either. Going back to the original Rosenbaum and Rubin article which first proposed the methodology for propensity scores, their theory held for assignment to the “control” group, which would be observed, however, the Vakulenko-Lagun et al have changed this into an unobserved probability of selection for truncation.
The simulation studies section made it easier to understand how their estimators for survival compared against previously developed estimators to deal with this issue of dependency between event times and left truncated times. In their simulations they demonstrate through Cox proportional hazard models and mention in their 5 guidelines of use of their methods that the assumption for this has to be met before employing their method. What is hard though to understand is how they can justify that the use of their methods in the Cox framework is not invalidating other assumptions like independence of event times and the non-informative general assumptions which would also affect the modeling. They even mention there may be informative censoring for their estimators. This does not seem well discussed in this article and it not mentioned as a weakness in the Discussion. Obviously, these article underwent peer review in Biometrics where it was published, but in just a first pass of the review of this article, I still feel there are important questions remaining about the justification and use of their theories. All in all, it is an important theoretical problem to address in survival analysis.
Written by,
Usha Govindarajulu
Keywords: survival, truncation, propensity, weighting, IPW, Cox model, censoring, informative
References
Rosenbaum, P. and Rubin, D.B. (1983) The central role of the propensity score in observational studies for causal effects. Biometrika, 70, 41– 55.
Vakulenko-Lagun B, Qian J, Chiou S H, Wang N, and Betensky RA. (2022). “Nonparametric estimation of the survival distribution under covariate-induced dependent truncation” Biometrics. 78(4): 1390-1401.
https://doi.org/10.1111/biom.13545
https://onlinelibrary.wiley.com/cms/asset/904a084b-b91a-4d7d-9fcd-6643cb5fddd9/biom13545-fig-0002-m.jpg