May 10, 2023
The authors Sun et al present a semi-competing risks framework using a flexible two-parameter copula-based semiparametric transformation model with interval censoring and left truncation. The semi-parametric transformation model allow both proportional hazards and proportional odds in both margins. Their data application, Chinese Longitudinal Healthy Longevity Study (CLHLS), pertains to disability, which is the main event, and then death and other causes became semi-competing risks.
The authors first laid out their copula model for semi-competing risks data, utilizing Archimedean copulas to model the marginal survival function for each terminal time event, in which the dependence can be expressed by Kendall’s tau parameter. They assumed interval censoring due to the convention in longitudinal studies for this. Also, they presented four possible scenarios for censoring due to different possibilities for when the event, disability, or the event, death, could occur and also possibility for left truncation. They next laid out an observed data and joint likelihood with left truncation in Equation 4 and covered all their possible censoring scenarios. The authors also employed a semi-parametric transformation model for the marginal survival function of time.
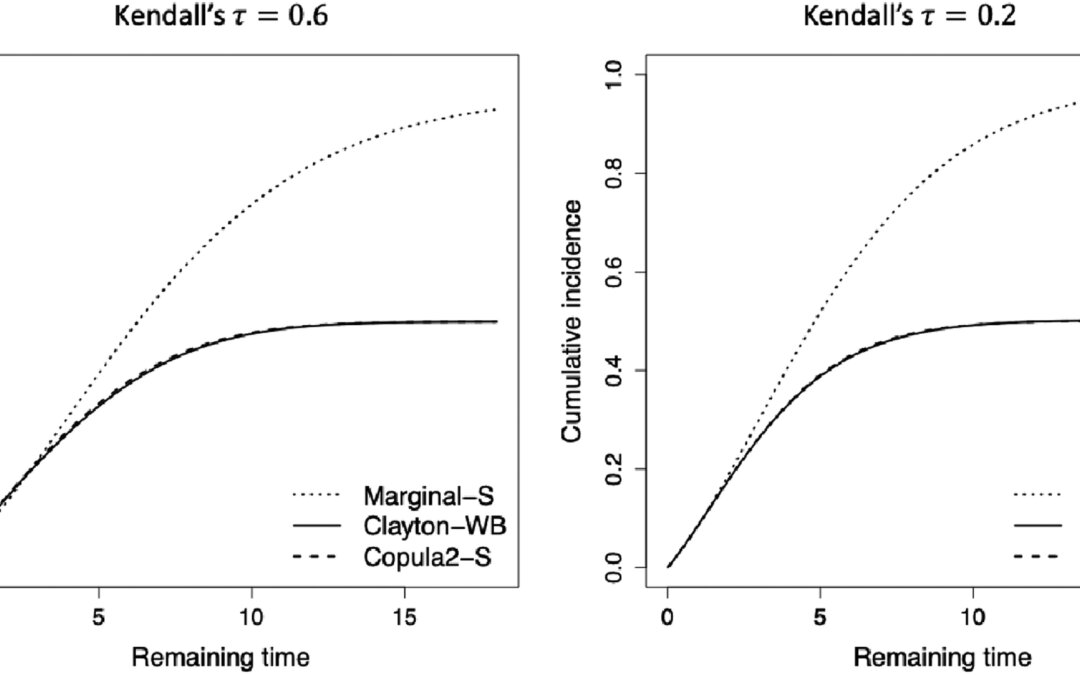
Finally, the authors discussed estimation and inference. They used a sieve likelihood with Bernstein polynomials, which is a method that can estimate infinite dimensional parameters and was applied to their interval censored data which had the absence of exact event times. The process used two steps and a pseudo likelihood function is estimated in the 2nd step which has to be done sinc the non-termnal event is dependently censored by the terminal event. They were then able to use standard optimization algorithms for the log-likelihood and obtain variances from the observed Fisher’s information. They then used a cumulative incidence function to estimate the marginal survival function for the non-terminal event, T1, over time which was estimated from a sieve maximum likelihood estimator.
Through simulations, the authors were able to test the models’ performances, also under special cases. Overall they found the performance of their model and the true models were close while the marginal model leads to biased estimation and incorrect coverage probabilities. They also tried copula misspecifications and still found in general their model performed fine. They finally demonstrated their method on a the CLHLS and showed hazard ratios for different covariates to show they had reduced risks of develop disability. This appeared to be a misinterpretation on the part of the authors about the HRs from their model and aligning this with risk when hazards are never risk. They claim the results of the copula methods align with the marginal model, which is hard to understand given the confidence intervals around their hazard ratios contained 1.0 while for the copula method, they were statistically significant.
In conclusion, the authors suggested their proposed method which is a flexible two-parameter copula-based semiparametric transformation model works for semi-competing risks data subject to interval censoring and left truncation. They have built this model into a R function, CopulaCenR. They do admit there were a lack of goodness-of-fit methods under interval censoring and so they had to rely on the AIC. The authors asserted that their semiparametric transformation model was better than making parametric assumptions which also affected the copulas, however they did admit that the PH/PO assumptions may not hold in practice. They chose those models since their parameters have interpretability, which can be a problem for non-PH or non-PO models. They mentioned they could have included a frailty effect to account for dependence between transitions but they stuck with the copula based modeling since the parameters have a straightforward interpretation. They further admitted that in the CLHLS real dataset application, they did not include any time varying covariates. They did not discuss that this was the only real dataset application and their simulations were geared around this so it may hard to know if their method truly generalizes.
Written by,
Usha Govindarajulu
Keywords: survival, left truncation, semi-competing risks, copula, transformation model, sieve method
References
Sun T, Li Y, Xiao Z, Ding Y, Wang X. Semiparametric copula method for semi-competing risks data subject to interval censoring and left truncation: Application to disability in elderly. Statistical Methods in Medical Research. 2023;32(4):656-670. doi:10.1177/09622802221133552
https://journals.sagepub.com/cms/10.1177/09622802221133552/asset/images/large/10.1177_09622802221133552-fig2.jpeg