March 13, 2024
New immunotherapies for cancer have shown to have different treatment effects often with delay compared to other cytotoxic treatments and, therefore, this has called for different ways of modeling the survival curves. The usual log-rank test has relied on the proportional hazards assumption for the test but delays in survival would cause violations in that assumption. Various alternatives have been proposed such as a weighted log-rank, restricted mean survival time, etc.. The authors proposed a technique that would have allowed for the delay and also crossing in curves, which theoretically has been a no go with proportional hazards assumption.
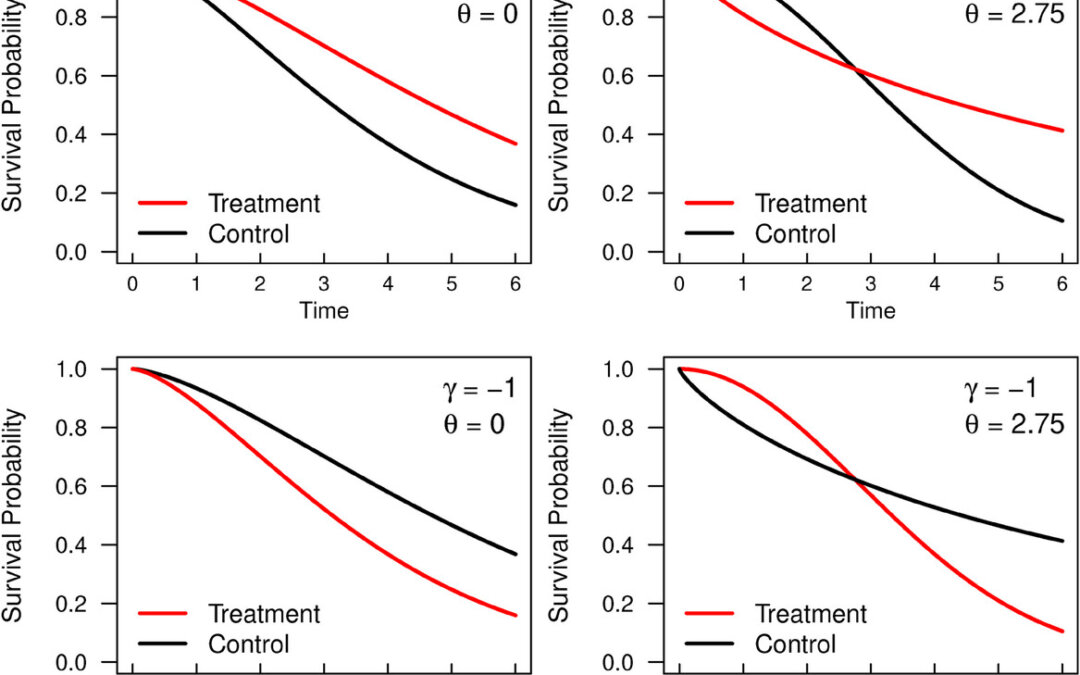
In the first stage, one finds conditional estimates of the survival function by maximizing a nonparametric log-likelihood that is conditional on the value of two crossing parameters. Then, in the second stage, one estimates these crossing parameters by maximizing a profile log-likelihood function. For the first part, they created a terms, theta and gamma, to represent crossing time. The authors then estimated survival under a non-parametric paradigm proposed by Park et al (2012). They only considered single crossing possibilities and non-smooth hazard possibilities. The authors then characterized ways to estimate the survival probabilities between the two curves. The first mentioned was at specific time points, which can avoid the proportional hazard assumption. The second was the proportion surviving up to crossing. The third was restricted mean survival time up to a particular defined time, tau. The fourth was restricted residual mean life. The fifth was crossing time conditional survival curves. Finally the last was pre and post crossing average hazard ratios.
They then had run simulations where they assumed survival followed a piecewise exponential distribution in both treatment arms and they showed six scenarios for different types of crossing curves. They found their methods of single-crossing constrained estimates of the survival curve in general performed better than a standard Kaplan-Meier based curve but this was not always the case in every scenario. They also tested this in a real data example and then in the discussion, they suggested their method may work better as a secondary analysis under condition of delayed treatment effects since they had an issue with robustness of model misspecification. They then discussed all sorts of other extensions or further possible developments for their method.
Written by,
Usha Govindarajulu
Keywords: survival, delayed treatment effects, Kaplan-Meier, log-rank test, restricted mean survival time
References
Henderson NC, Nam, K, and Feng D (2024). “Nonparametric analysis of delayed treatment effects using single-crossing constraints” Biometrical Journal. https://doi.org/10.1002/bimj.202200165
Park, Y., Kalbfleisch, J. D., & Taylor, J. M. (2012). Constrained nonparametric maximum likelihood estimation of stochastically ordered survivor functions. Canadian Journal of Statistics, 40(1), 22–39.
https://onlinelibrary.wiley.com/cms/asset/941bc966-1829-4bad-bd83-4caf1e3c7434/bimj2560-fig-0001-m.jpg