November 9, 2023
In this article that appeared in a special issue in the Biometrical Journal, Morelle et al described a joint modeling approach to account for the longitudinal followup of patients at subsequent hospitalization or competing risk. While most prognostic scores ignore biomarker changes over the time, the proposed model by the authors incorpoate the longitudinal biomarker changes over time by use of a nonlinear mixed effect model that allow biomarker change as well as a survival model describing hazard evolution. The authors used real data of patients who were hospitalized for SARS-CoV-2 infection. They compared this model against a model that only used baseline information.
The real data comes from patients who had been hospitalized in an academic hospital in France. The primary outcome was a time to event of death with competing event of discharge. They used the subdistribution framework for the competing risks. They created subdistribution risks and then used a linear link between those and the longitudinal process. Thus, the structural model was a linear mixed effects model or a nonlinear mixed effects model. They tended to use the latter. Since they had no way of computing their likelihood, they had to use the SAEM algorithm implemented in Monolix software.
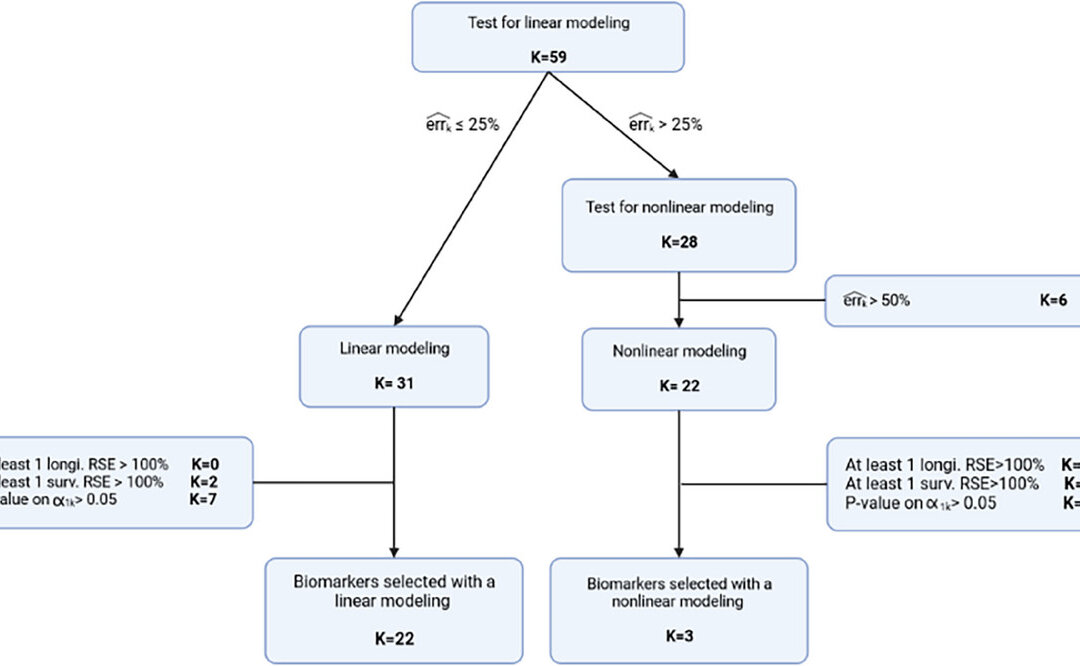
They started the individual modeling of the biomarker using estimates from a no link model, and then proceeded to a error model selection for each biomarker, using Bayesian Information Criterion to select each model. Only the biomarkers with error less than 25% were kept for the joint model. Biomarkers with a large error were then evaluated using a nonlinear longitudinal model. If biomarkers had a measuremnet error larger than 50% or with at least one RSE of a longtiduinal parameter over 100% then they were excluded. The last step was evaluating the survival model. The first involved good quality of survival parameter estimation. The second was a link between the longtiduinal process and the instantaneous risk of death which were selected via a Wald test. The biomarkers selected at the univariate stage were grouped according to most significant p-value and then a subset of these were selected based on backward selection criterion using the Wald test highest p-value to be removed.
Dynamic predictions were done based on a conditional probability definition. The baseline model and the multivariate model were compared by time-dependent receiver operating curve characteristic area. They evaluated their method in both real data and simulated data. They also evaluated their backward selection method in the simulations, which was good as this seemed questionable due to evaluations with p-values. They found that even with more correlated biomarkers that the method worked well. However, later in the Discussion section, the authors did admit that the backward strategy could lead to more computational time for an already computatinoally intesnive process and they later suggested that using penalied methods could have been better in this situation. They did not discuss the use of Cox models in the survival part in terms of the advantages or disadvantages of this.
Written by,
Usha Govindarajulu
Keywords: survival, multivariate joint model, linear mixed model, competing risks, Sars-CoV-2
References
Lavalley-Morelle A, Peiffer-Smadja N, Gressens SB, Souhail B, Lahens A, Bounhiol A, Lescure F-X, Mentré F, and Mullaert J (2023). “Multivariate joint model under competing risks to predict death of hospitalized patients for SARS-CoV-2 infection” Biometrical Journal.
https://doi.org/10.1002/bimj.202300049