September 11, 2024
This article focused on joint modeling in the presence of informative censoring in a retrospective analysis in palliative care research. There has been a lack of statistical models to handle longitudinal quality of life (QOL) data and survival data. Another challenge has been the handling of the dropouts in the palliative care studies. As the dropouts have been associated with QOL and survival then they are called informative dropouts which leads to informative censoring. This has remained an issue for modeling longitudinal data on the retrospective scale since time points of longitudinal data are unknown on the retrospective scale, when death is censored. Meanwhile the censoring time would have been associated with the longitudinal data and death time. Terminal trend models (TTM) have already been proposed to jointly handle analyzing longitudinal QOL data and survival data in palliative care studies and then have had advantages to estimate QOL on the retrospective time scale, but under the assumption of non-informative censoring. To fill the gap, the authors then developed a new semiparametric model under the TTM framework to analyze data in palliative care studies or other studies that have possible short life expectancy.
Their model has two submodels: a semiparametric mixed effect submodel for the longitudinal QOL data and a competing-risk survival submodel with piecewise hazards for the death time and the dropout time. The mixed effect submodel has used splines to model the longitudinal trajectory and therefore handle linear or non-linear curves. The piecewise hazards have allowed variation in the hazards over time. Both submodels have shared a common random effect used to handle association between dropout time, QOL, and death time. Although the authors had not immediately indicated, the random effect term they included is a frailty term which they denoted later in their notation for the hazard for the competing risk. Essentially, the submodels for death time and dropout time were frailty models that share the same random effect with the submodel of the longitudinal QOL. In their model, the parameter estimation was done with regression splines using knots placed at quantiles equally spaced at the observed times of the longitudinal measurements.
They found that for the joint models on the prospective time scale that the M-step of the EM Algorithm usually had a closed-form solution for the coefficient and the variance parameters of the longitudinal submodel and the cumulative baseline hazard of the survival submodel. Also, they used one-step Newton-Raphson method to update coefficient parameters of the survival submodel. They used Gauss -Hermite quadrature approximations for the integrations. But due to computational challenges with using the EM algorithm, they proposed to directly maximize the log-likelihood function to obtain the MLE. In order to choose optimal number of knots for the regression splines, since they have a log-likelihood, they used AIC selecting optimal number of knots since it puts a smaller penalty than BIC on the number of parameters so then the set of knots that minimized the AIC statistic ended up being their set of optimal knots.
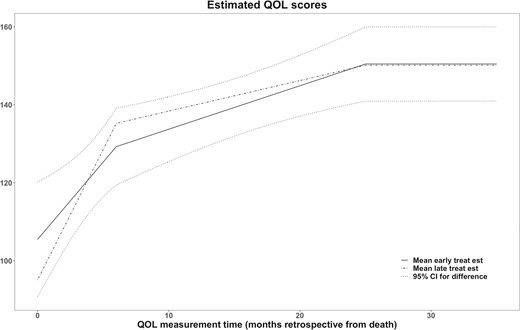
They ran simulations and also on a real dataset application. They said their simulations demonstrated that their model had better performance with respect to bias and coverage probability in the presence of informative censoring as compared to previous methods. They did admit in their discussion they could have used cubic splines instead of linear splines and they could have removed the normality assumption on the random effect in order to have a fully nonparametric random effect. To reduce computational time, they included only one random effect and they tried to reduce the number of knots.
Written by,
Usha Govindarajulu, PhD
Keywords: survival analysis, longitudinal, survival, competing risk, frailty, mixed-effects
References
Quran Wu, Michael Daniels, Areej El-Jawahri, Marie Bakitas, Zhigang Li, “Joint modeling in presence of informative censoring on the retrospective time scale with application to palliative care research”, Biostatistics, Volume 25, Issue 3, July 2024, Pages 754–768, https://doi.org/10.1093/biostatistics/kxad028
https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/biostatistics/25/3/10.1093_biostatistics_kxad028/2/m_kxad028f3.jpeg?Expires=1729009418&Signature=Ye29ZgyE~BfCRKQpzImgYgoXd3zTIYdUlUiUIgY8BwCJnye90Y9zibA0UnH-hBbN0HgWvSakTxd4CtG1J-DwIurDdMPhBhnM4kRnYoymMtx0WkbODigUrjq~Sxm7sj0pqrTIa-wSN5L38o9K8UkqAy3j8YjBYQs4u3jS9FgvgUbkJXUPfQ-i9iu5y03T8nVp-crjWG2jonMzqHmUPNSPtG9nSm8aVdFy47A2Aa99vDYIejHlFf~fzVZlzjwurTuLFAkggHeC8bIM7w3Y4ya7KarzT7ixdqon734xokVFanuUXCl06cNcMeKLtzG9qwOJ~7gw36FA2Y~Zxjnn45cx2g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA