November 20, 2024
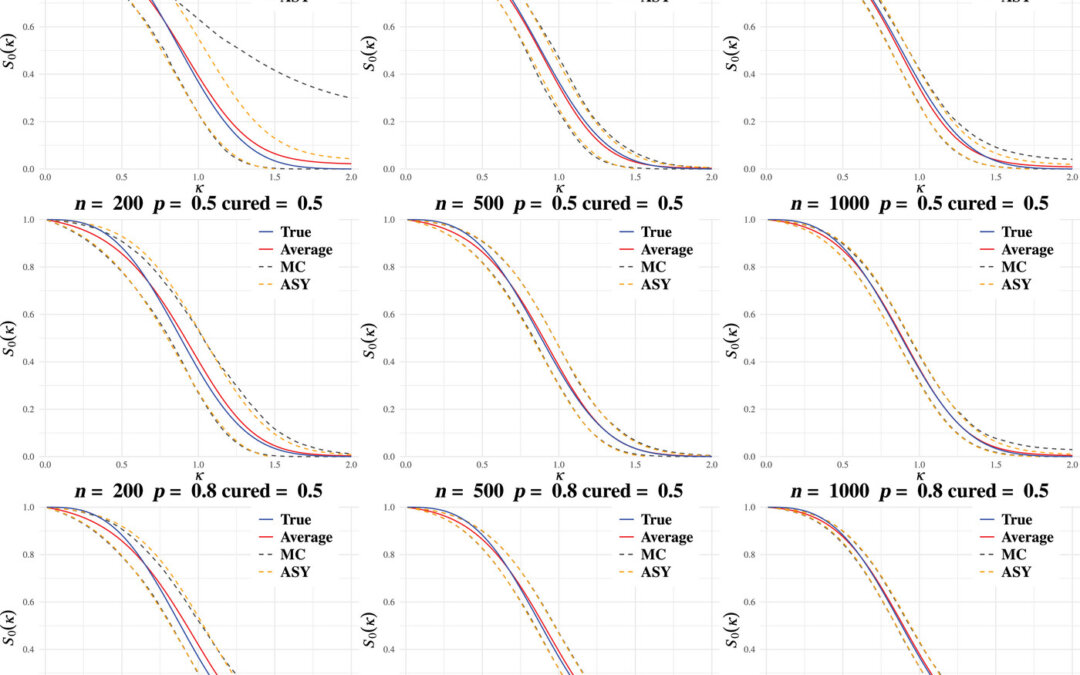
Most of the literature on mixture cure models has focused on using Cox proportional hazards regression for the basis of the model, but the proportional hazards assumption over time can make this difficult, therefore, the authors have focused on using the accelerated failure time model (AFT). They also preferred the AFT since it focuses on estimating survival rather than hazard and they estimated a smoothed estimate of the baseline survival function via estimating the baseline hazard function. For the cure probability, they used a logistic model where gamma parameters were the main coefficients describing the incidence. In estimating the baseline hazard, they found that methods like M-or B-splines were not useful since they require specification of the boundary knots so they instead focused on Gaussian basis function also known as a Gaussian kernel. In order to fit their mixture cure AFT model, they maximized the log-likelihood function using a roughness penalty function. However, they used an iterative alternating algorithm which employed quasi-Newton schemes to update beta and gamma parameters first followed by a multiplicative-iterative (MI) scheme. A marginal likelihood method for estimation of σ2θ required integrating out all the other parameters from the posterior density, but they had to use a Laplace method to approximate this integral due to problems obtaining a closed form solution.
In simulations, they compared their MPL method to the EM-based approach in the R package, smcure, using right censored data only since the latter package could only handle that. They did find that while the MPL method was doing well that both methods suffered from an identifiability issue due to estimating gamma parameters from s logistic model for cured patients and the AFT model beta coefficients for latency. They believed overall their MPL method outperformed the R smcure package. They have implemented their method in an R package, aftQnP.
Also, reliable estimates of the intercept of incident required a high event proportion. They could have addressed this if they correctly identified the zero tail for the noncured group, but they believed the Gaussian basis functions have difficulty with this near the boundaries and so then they mention that B-splines or M-splines would have been useful in this context, yet these are the splines they decided not to use because they require estimation of boundary knots. They still need to address the identifiability issue and discussed some options like using Weibull or exponential distribution for the survival tail function or in the current model to employ a different kernel as the last basis function which would decay more rapidly. Eventually they want to extend the model to longitudinal data.
Written by,
Usha Govindarajulu, PhD
Keywords: survival, AFT, mixture cure model, splines, R software
References
Li I, Ma J, and Liquet B (2024). “Mixutre Cure Semiparametric Accelerated Failure Time Models with Partly Interval-Censored Data” Biometrical Journal.
https://doi.org/10.1002/bimj.202300203
https://onlinelibrary.wiley.com/cms/asset/e707c14d-0029-46e5-8c0a-69f1353501aa/bimj2621-fig-0001-m.jpg