December 31, 2025
Count data are collected in many different types of experiments, yet their analysis remains challenging, especially in small sample sizes. Until now, linear or generalized linear models (GLMs) with either a Poisson or Negative Binomial distribution have often been used. However, these data frequently show signs of over-, underdispersion, or even zero-inflation, which lends less authenticity to these distributional assumptions and can lead to inaccurate test results. Since their distributions are usually skewed, data transformations (e.g., log-transformation) are frequently implemented. As the authors pointed out, this underscores the need for statistical methods not to hinge on specific distributional assumptions.
They also investigated multiple contrast tests that allow general contrasts (e.g., many-to-one or all-pairs comparisons) to analyze count data in multi-arm trials. Multiple comparisons to control or testing Grand-Mean contrasts, are of interest and will be implemented using multiple contrast test procedures (MCTPs) (Bretz et al. 2001; Konietschke et al. 2012).
They aimed to investigate the impacts of (a) model misspecification on various MCTPs in small sample sizes and (b) data transformations on the behavior of MCTPs. In addition, they also employed the impact of the usual Poisson and Negative Binomial distributions but also of another less prominent candidate, the Conway–Maxwell–Poisson distribution, on existing and novel test procedures.
The authors also discussed model misspecifications which come up in practice. Most models assume homoskedasticity of variances so dealing with heteroskedastic variances for count data in GLMS can be problematic. They did recommend a White’s heteroscedasticity-consistent sandwich-type estimator (White, 1980) to handle this when doing contrast tests. They also investigated count data that was transformed through data transformation as well as the impact of differently assumed distributions (Poisson, Negative Binomial, and Quasi-Poisson) on the contrast tests from generalized linear models. They estimated these through the R package, emmeans. They also employed a non-parametric bootstrap test for estimation of the variances.
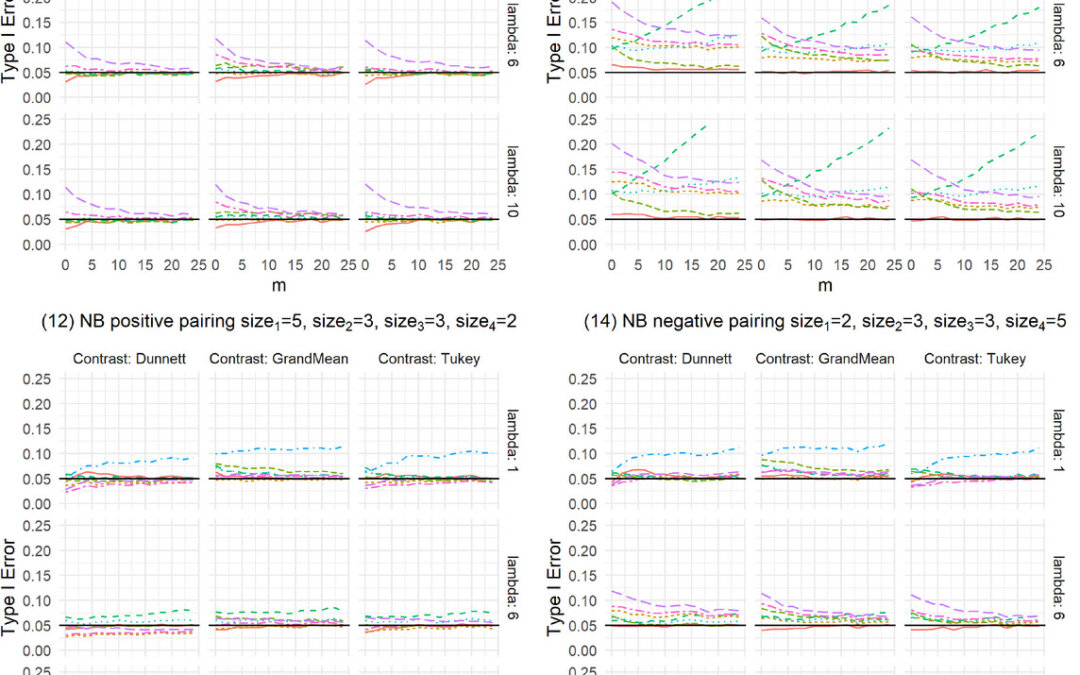
In their simulation study, all the methods they investigated were asymptotic and, therefore, accurately control the Type I error level when sample sizes are large. This led then to an interest when the sample size is small. They then evaluated Type I error control and power, also while varying count data distributions: Poisson, Negative Binomial, and Conway-Maxwell-Poisson (CMP) distributions. They also varied the dispersion parameters for these distributions. The Negative Binomial can only handle over-dispersed data while the CMP can handle both over- and under-dispersed count data.
They found that no single method controlled the Type I error rate best in all examined settings. The allocation of dispersion and rate parameters strongly affects the Type I error rate. There were some recognizable differences between the methods for global power. The results of the simulations suggested that no single method performed best across all investigated settings but the bootstrap test and the linear model with heteroscedastic variances performed well in most settings examined.
Written by,
Usha Govindarajulu
Keywords: count data, multiple contrast tests, small sample, generalized linear models, Poisson, Negative Binomial, dispersion, non-parametric bootstrap
References:
Bretz, F., A. Genz, and L. A. Hothorn. 2001. “On the Numerical Availability of Multiple Comparison Procedures.” Biometrical Journal 43, no. 5: 645–656. https://onlinelibrary.wiley.com/doi/10.1002/1521-4036(200109)43:5%3C645::AID-BIMJ645%3E3.0.CO;2-lF.
Konietschke, F., L. A. Hothorn, and E. Brunner. 2012. “Rank-Based Multiple Test Procedures and Simultaneous Confidence Intervals.” Electronic Journal of Statistics 6: 738–759. https://doi.org/10.1214/12-EJS691.
Pigorsch M, Hothorn LA, and Konietschke F (2025) “Multiple Contract Tests for Count Data: Small Sample Approximations and Their Limitations” Biometrical Journal.
https://doi.org/10.1002/bimj.70098
White, H. 1980. “A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity.” Econometrica: Journal of the Econometric Society 48, no. 4: 817–838. https://doi.org/10.2307/1912934.
https://onlinelibrary.wiley.com/cms/asset/013c66e2-dfce-467e-b621-5541cf2edda8/bimj70098-fig-0006-m.jpg