October 8, 2025
Mixed effects logistic regression models require individual level data. Sometimes data needs to be on the population level and it can be aggregated into counts, for example, but this could also lead to loss of other information. Federated learning has emerged as a better solution to fit models using data from multiple hospitals without requiring sending individual level data. For generalized linear mixed models (GLMM), including logistic regression with random intercept, federated learning algorithms have been developed. These algorithms rely on strategies like distributed versions of the penalized quasi-likelihood method. Another approach which can further reduce need for iterative communication with data providers is a noniterative approach which accommodates both categorical and continuous covariates which is based on artificial data generation using a Gaussian copula. The authors have proposed their own noniterative method based on previous ideas by generated pseudo-data to match summary statistics of the original data and then allowing for estimation of logistic mixed models without requiring iterative communication. Their approach can also accommodate multiple covariates and it uses Gauss-Hermite quadrature (implemented in the R software) to estimate the likelihood of a GLMM which they feel is more accurate than using a penalized quasi-likelihood method.
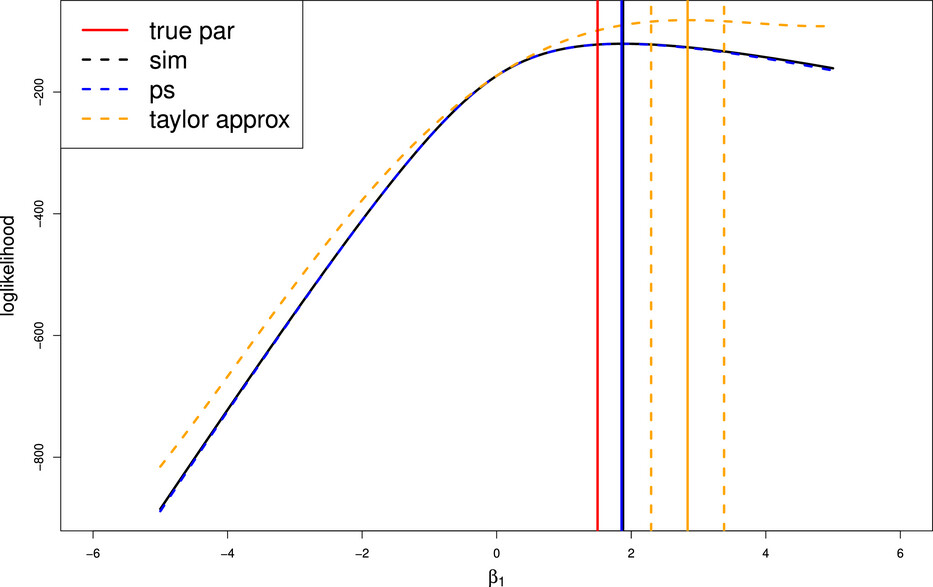
A requirement of their strategy is that the data providers (i.e. hospitals) supply the data analyst with privacy-preserving summary statistics. Also it is assumed these were generated with no missing data. They refer to summary statistics that could be exact sufficient statistics or polynomial-approximate sufficient statistics. For polynomial approximation one can use the Taylor expansion and then can express the log-likelihood as a K-degree Taylor polynomial plus an error term. These polynomial-approximate sufficient statistics are the summary statistics expected from each data provider to proceed with model estimation and not having to disclosure individual level data. For a binary variable, one can follow the same formulas they showed by compute central moments by the Taylor polynomial expansion while with categorical predictors with more than two levels, one must convert them into dummy variables before computing central moments.
They then proposed generating pseudo-data from the polynomial-approximate sufficient statistics and then using these in place of actual data. They did not aim to reconstruct the actual data as they want to protect privacy but to still in a way mimic the actual data without giving away any identifiers. To match the summary statistics, they applied a concept of nonlinear least squares optimization with the goal being to minimize the sum of squared differences in the summary statistics between the pseudo-data and the actual data. They used the Levenberg-Marquardt method to solve this optimization problem. Their steps are essentially to generate binary pseudo-data for the response variable based on sample proportion of events and then for the predictor to generate pseudo-data as means for each based on summary statistics from the actual data. Their code to generate pseudo-data was developed in R via the lsqnonlin function from the package, pracma. In order to generate data for mixed-effects logistic regression this entails generating pseudo-data for the actual unavailable data through their summary statistics and this has to be done for every cluster or data provider.
They ran simulations and used the glmer function from R to estimate multilevel logistic regression since it implements the Gauss-Hermite quadrature. They also assessed when there was variable omission, misspecified random effects distribution, and variable omission with large random effect variance. They found pseudo-data matching had differences matching up to the fourth moment and mimicking interval estimates derived from simulated data for larger covariates effects but only when the cluster size is small. The coverage for the pseudo-data was mostly fine for the first through fourth moments. Overall their results for the correctly specified models showed the pseudo-matching up to the 3rd moment achieved the most similar performance with the simulated data in terms of bias, coverage, and AIC values. In misspecified models, their method worked as well as in the correctly specified models scenarios except when the random effect term variance was significantly increased.
Their real dataset analysis with data from CHOP shows how they generated pseudo-data from multiple wards which was data from during COVID-19. The pseudo-data analysis was very similar to the actual data analysis.
Written by,
Usha Govindarajulu
Keywords: mixed effects logistic regression, federated learning, GLMM, Taylor expansion
References:
Limpoco MAA, Faes C, and Hens N (2025). “Federated Mixed Effects Logistic Regression Based on One-Time Shared Summary Statistics” Biometrical Journal
Zhao, Y. (2025) “Unified Estimation Method for Partially Linear Models With Nonmonotone Missing at Random Data” Biometrical Journal. https://doi.org/10.1002/bimj.70070
https://onlinelibrary.wiley.com/cms/asset/e91a7d46-5115-4dc4-9a74-8e2fe30ef685/bimj70080-fig-0001-m.jpg