March 26, 2025
Their primary goal of their paper was to introduce a novel frailty model based on the weighted Lindley (WL) distribution for modeling clustered survival data. They used the weighted Lindley as the frailty distribution. This was a two parameter distribution where the main statistic is always on the positive real line. This distribution allowed lot of flexibility more so than other distributions. It is useful for modeling right-skewed data and bathtub hazard shaped data as well as bimodal data, which lot of other typical frailty distributions cannot handle.
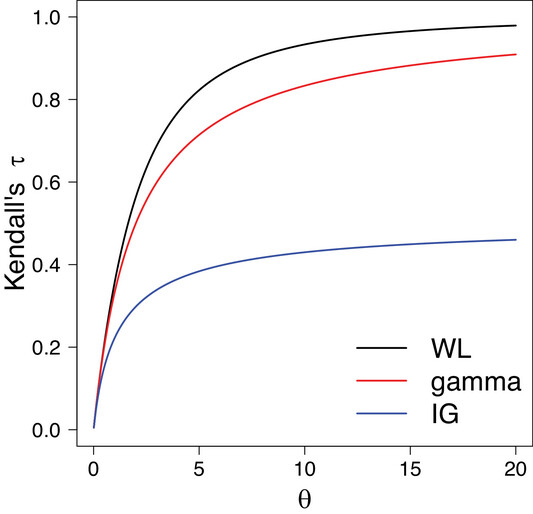
The WL distribution can be denoted as a mixture of two gamma distributions with weights. They also showed a version where the mean is fixed at 1 as typically done for the frailty distribution in analyses. They used Laplace transforms for which they had closed form solutions for the derivatives. They also wrote out the univariate and the shared frailty, to allow for clustering, versions of the WL frailty model. They used Kendall’s tau to calculate the product of difference between survival times to calculate that correlation. An alternative transform was based on the Laplace transform of the frailty distribution. They found for a fixed variance for the frailty, the WL provides a greater Kendall’s tau as compared to the gamma or inverse Gaussian frailty models. They then showed a modified EM Algorithm for estimating their model. They used a Cox model with an offset term for natural log of the frailty and then they iterated their E-step and M-step until they reached their convergence criterion. The authors had previously developed an R package, extrafrail to include computational implementation for the WL frailty model which considers the baseline model the WEI distribution and the semiparametric specification.
They then conducted simulations to see if the ML estimators were well estimated in finite samples under different scenarios and to also assess the performance of the model with misspecification in the frailty distribution. They also fit their model on a real dataset of rehospitalization times after surgery in patients with colorectal cancer. They found overall their new method was quite robust in estimating covariates effects as well as the frailty variance. Their model has offered mathematical tractability, flexibility, simplicity, and computational attractiveness. They plan to explore other estimations of the model like by a Bayesian approach. Also the model can be extended to the case of time-varying frailty and the WL frailty model with a cure fraction.
Written by,
Usha Govindarajulu
Keywords: survival analysis, Lindley frailty model, clustering, Laplace transform, Kendall’s tau
References:
Gallardo DI, Bourguignon M, and Santibáňez JL (2025) “The Shared Weighted Lindley Frailty Model for Clustered Failure Time Data” Biometrical Journal, https://doi.org/10.1002/bimj.70044
https://onlinelibrary.wiley.com/cms/asset/fc676d8f-a347-41ad-9773-fb4fcf845363/bimj70044-fig-0001-m.jpg