October 15, 2023
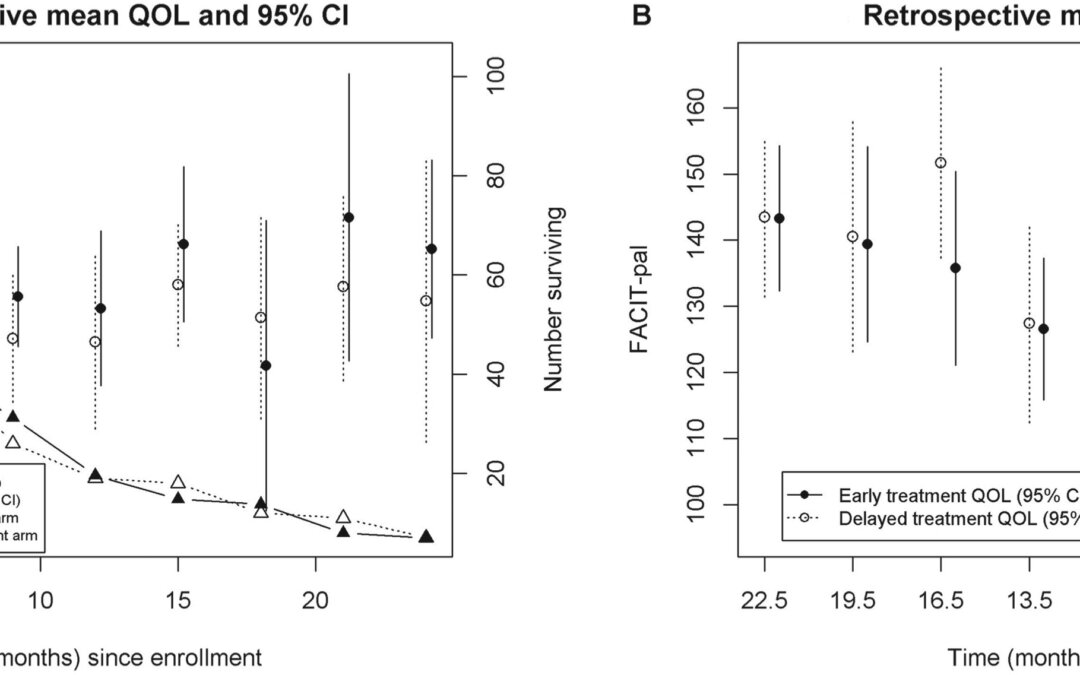
The authors discussed how to handle model joint survival and longitudinal modeling in the presence of informative censoring caused by informative dropouts by participants in a study. The authors framed this in terms of palliative care studies where the quality of life (QOL) is the longitudinal portion of the study which had dropout. To fill this void, they developed a new semiparametric model for analyzing data in palliative care studies or other studies with relatively short life expectancy. Their joint model shown has two models: a semiparametric mixed effect submodel to handle the longitudinal QOL data and a competing risks survival submodel with piecewise hazards for time to death and dropout time. They modeled death and dropout as competing risks rather than censor dropouts. Their mixed effects models used splines for the longitudinal trajectories, linear or non-linear.
In the setup for their model, they calculated the administrative censoring time as the duration between the study completion time and and the enrollment time so that time is either chosen per subject as the death time, dropout time, or administrative censoring time and death and dropout are treated as competing risks. The model was written in mixed effect modeling format, where they used a piecewise-exponential competing risk model for time to event data with a frailty term at the individual level, which is the same random effect term used in the longitudinal model. The model also had separate baseline hazard functions for each competing risk. They used regression splines on the non-parametric functions that appear in the mixed effects model format, using the same knots for the three function at equally spaced quantiles. The splines they used had linear spline basis functions, but no justification for this choice of basis function was provided as to why they chose linear. The optimal number of knots were determined by use of Akaike’s Information Criterion, which they decided to use instead of the Bayesian Information Criterion since it uses a smaller penalty on the number of parameters. The authors then showed one way of analyzing the log-likelihood and then an alternative way using an EM algorithm but treating the random effect as missing data, where in the M-step, a closed form solution for coefficient and variance parameters should occur for the longitudinal submodel and the cumulative baseline hazard of survival submodel. Thereafter, a one-step Newton-Raphson method could be used to update the coefficient parameters of the survival submodel. All their integrations were done with Gauss-Hermite quadrature approximations. They did not have closed form solutions at the M-step so it became quite computationally demanding. Therefore, they then proposed to directly maximize the log-likelihood function to obtain the MLE.
In simulations, they compared their approach with the naïve approach and the non-informative censoring approach. They found their approach was more efficient as compared to either of these two approaches in terms of coverage probability and bias as measured through coefficients. They also tested their model on a real data application. In their discussion, they did admit the splines could be extended to cubic splines (i.e. B-splines) instead of linear splines but that it could be more time-consuming to calculate the integrals for groups 2 and 3 without explicit formulas for calculation of nested integrals. At the end of their discussion that they admit that although their modeling can accommodate a broad range of of longitudinal trajectory patterns by employing linear splines, when there are noncontinuous longitudinal trajectories, they recommend case wavelet-based models (Morris and Carroll, 2006) could be adopted for analysis instead.
Written by,
Usha Govindarajulu, PhD
Keywords: survival, longitudinal, informative censoring, splines, mixed model, hazard
References
Morris, J. S., Carroll, R. J. (2006). Wavelet-based functional mixed models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68, 179–199.
Quran Wu, Michael Daniels, Areej El-Jawahri, Marie Bakitas, Zhigang Li, Joint modeling in presence of informative censoring on the retrospective time scale with application to palliative care research, Biostatistics, 2023;, kxad028, https://doi.org/10.1093/biostatistics/kxad028