December 6, 2023
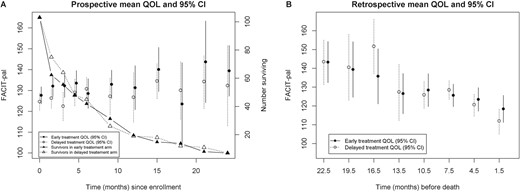
In article that appeared in Biostatistics, Wu et al describe a joint modeling approach of longitduinal data like quality of life and survival data on a retrospective time scale and handling of informative censoring issues in a two arm clinical trial setting. These have been handled on more of a prospective time issue, but much less retrospectively. One of the biggest issues has been handling dropouts in a joint modeling on a retrospective time scale. They have proposed a semiparametric modeling that jointly models longitudinal QOL data, death time, and informative censoring time. It has used a semiparametric mixed effect submodel for the longitudinal QOL data and a competing risk survival submodel with piecewise hazard for time to death and dropout time. The mixed effect submodel used splines to allow for potential non-linearity. Their model incorporated a frailty term in the hazard function for the competing risks model. Even the frailty component was shown to have separate coefficients for each piecewise exponential. They then wrote out this piece as a Cox model with the baseline hazard rate represented as two separate pieces for the competing risks and then combine this with the longitudinal mixed model as the final longitudinal model. They then used regression splines with equally spaced knots at quantiles to estimate the parameters.
They had to calculate the log-likelhood across six groups based on the delta that the particpant was in or rather based on their survival event status. They then had six log-likelihood functions to estimate which could create computational complexity. Therefore, an alternative way to estimate the MLE’s for each parameter was to use an EM algorithm, where the random effect term for frailty gets treated like missing data. One problem was that due to the retrospective nature of the data that the integrations in the M-step of the algorithm did not have closed form solutions due to unknown time origins for groups 2 and 3 where the death times were censored but integration of death time is needed to construct a log-likelihood function. They then said since the EM algorithm would have had computational challenges that they suggested directly maximizing the log-likelihood function to obtain the MLE.
They also discussed the optimal number of knots for the regression splines, for which they decided to use the AIC or BIC due to their having a log-likelihood function. They used the AIC since it generally puts a smaller penalty on the number of parameters than the BIC. I am not sure whey they had focused on linear splines only. They later mentioned in their discussion that they could have extended their model to use cubic splines (like B-splines), but the cubic splines due have more degrees of freedom and would make calculating the integrals for groups 2 and 3 more difficult. They mentioned some ways to deal with this, one of which was removing the normality assumption on the random effect term, making it unspecified.
Overall their method seemed to have worked well in simulations and real data and can be extended to other applications with QOL data from retrospective collection. They however never discussed their reliance on Cox modeling for the submodel and anything about the proportional hazards assumption. The authors, of course, have many areas of which they can still extend this research.
Written by,
Usha Govindarajulu
Keywords: survival, longitudinal, dropout, retrospective, mixed model, Cox model, linear splines
References
Quran Wu, Michael Daniels, Areej El-Jawahri, Marie Bakitas, Zhigang Li, Joint modeling in presence of informative censoring on the retrospective time scale with application to palliative care research, Biostatistics, 2023;, kxad028, https://doi.org/10.1093/biostatistics/kxad028
https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/biostatistics/PAP/10.1093_biostatistics_kxad028/1/m_kxad028f1.jpeg?Expires=1704842730&Signature=2KLhNYMoOKTU0uMSX9gsDOL5vhDL7g9ADZUVcNrVapRw0nnKRN856biqi5tlI6WsSnYEcg6nlKYYdgQnkIGkuoWSOwuMXjjig2XstqxdsGtvdQ3lU3EbeocvEhsXO04sIkKjTyJ7oCyEVIyik3~EhCjshfIiXc7yMgqsb1lbS7JPMGnWuljjTaa6xMOJOm~F86vIEtzc3SCfLJTjtoG78ByMKbF3AylLoURIWxNSstfoZAz3v6wDFGI69QKAUS5c4ynktWJyjqBGKodFmekycP9~5k4DEjxcDDGxZy2UEuB3oInfT~3R-i38ibSOGGDTC53CKOeLVR730giBrw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA