December 20, 2023
In article that appeared in Statistics in Medicine, Denz et al explored different methods for modeling of adjusted survival curves especially in observational studies, which tend to have issues with confounding. The authors also brought in causal inference and discussed a counterfactual survival curve or confounder-adjusted survival curve, which represents the survival probability that would be observed in the target popoulation, if every person in the population had received treatment Z. Therefore, the average treatment effect becomes the difference or ratio between two treatment specific counterfactual survival curves. Randomized controlled clinical trials have been the gold standard for the estimation of these types of curves since randomization ensures the it ensures that the distribution of covariates does not differ between groups with respect to treatment. If there is no randomization, then one has to meet these assumptions: stable unit treatment value (survival time of one persons is independent of the treatment assignment of other people in the study), no unmeasured confounding (all relevant confounders have been measured), and the positivity assumption (each person has a probability greater than 0 and less than 1 for receiving the treatment, z).
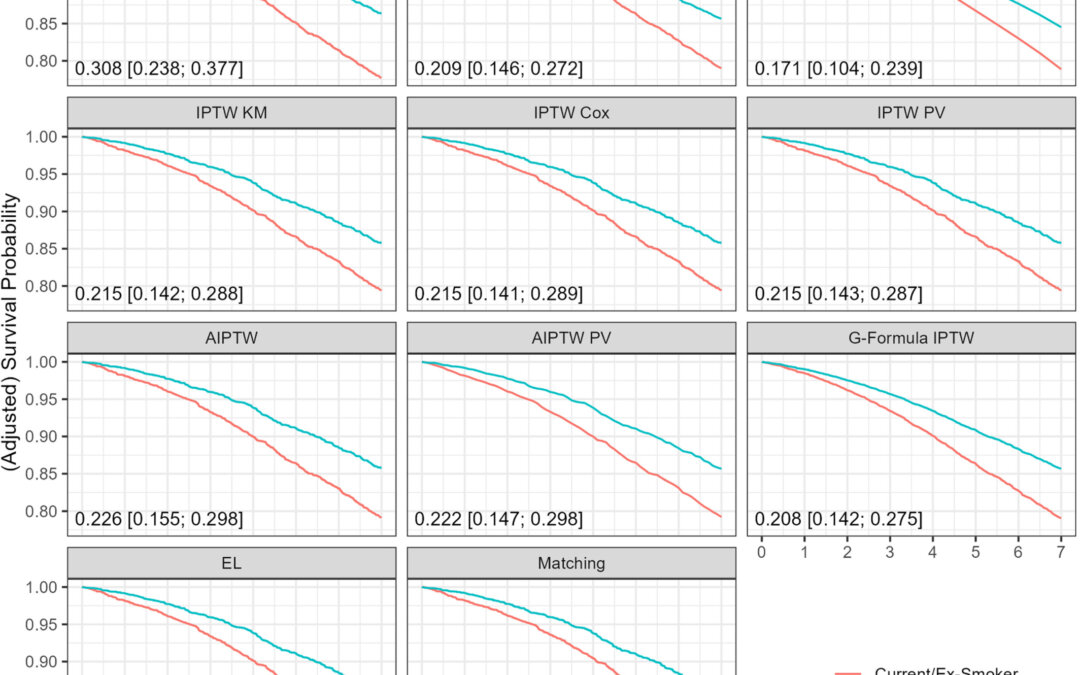
However, the authors had chosen to focus on the more difficult situation of observational studies. They focused on four methods used to adjust survival curves for measured baseline confounders when random right censoring is present. There were several methods which they chose to ignore for this paper, even the Targeted Maximum Likelihood Estimation based methods as they are only defined for discrete-time survival data, and as they mentioned, these methods have been shown to not work very well in practice. Thus, they focused on the G-Formula, Inverse Probability of Treatment Weighting (IPTW), Propensity Score Matching (PSM), Empirical Likelihood Estimation, Augmented Inverse Probability of Treatment Weighting (AIPTW), and their Pseudo Values based counterparts. They also compared everything against a standard Kaplan-Meier estimator. They categorized the methods of interest above into three categories: methods which utilize the outcome mechanism, methods that use the treatment assignment mechanism, and methods that rely on both mechanisms. For survival analysis, using outcome mechanism refers to modeling the process which determines the time to even to interest, while the treatment assignment mechanism describes the process by which an ith individual is assigned to one of k possible treatment where the goal is to estimate the probability of receiving treatment, z, for each individual, P(Z=z | X), which is formally known as a propensity score. This score has to be estimated from a model.
They described in some detail some of the main methods considered. The G-Formula or G-computation is where the confounders are adjusted by correctly modeling the outcome mechanism. The IPTW has utilized the treatment assignment mechanism for confounder adjustment. It has involved calculating propensity scores from a model like logistic regression where the treatment or exposure is the binary outcome in the model predicted by all possible confounder, and then the inverse of this probability score is calculated and then used as weights in new analyses. This has been though to remove the confounding and allow for ascertainment of the actual causal effect. However, previous research has shown IPTW to be less efficient than G-Formula. Meanwhile, the PSM has been shown to be less efficient than both IPTW and G-Formula for time-to-event analyses. The AIPTW was invented as using the G-Formula estimate to augment the IPTW estimate for efficiency. However, the AIPTW potentially could suffer issues with efficiency if models are incorrectly specified, have estimates monotonically decreasing, and estimates not be between 0 and 1, but no one has had the knowledge of how often this occurs in practice. Finally, another way mentioned was to combine the G-formula with the IPTW, but the research on this has not been fully cemented. Another method they discussed was an Empirical likelihood (EL), which is a constrained likelihood allowing for the moments of the covariates to be equal between groups. The last method discussed were pseudo values (PV), which can be created for each person at a fixed set of points in time and then used to construct G-Formula, IPTW, and AIPTW estimates of the survival curve. For the G-Formula, a generalized estimating equation with the PVs as the response variable can be fit with baseline covariates as predictors in the model and then used to obtain the conditional survival probability predictions. For an IPTW estimate, a PS weighted average of the PVs can be used.
To show applications of all these methods, they used the German Epidemiological Trial on Ankle-Brachial-Index, a prospective observational cohort study of 6880 primary care patients aged 65 and older. They found that the adjusted survival curves from the methods considered were closer to each other than the crude Kaplan-Meier curves. They also considered a simulation study in which they specified various scenarios with varying correct or incorrect outcome mechanism or treatment assignment. Basically, all eight methods produced unbiased estimates for the whole survival curve in simulated datasets with medium to large sample sizes. The AIPTW was similar to IPTW or outperformed it when both models were correct. However, the G-Formula IPTW method was found to not have the doubly robust property when trying to estimate the counterfactual survival curve, perhaps due to the addition of weights leading to a violation of the proportional hazards assumption. There was consistently a systematic bias in methods relying on Cox model in small sample sizes, even when it was consistenly estimate. Also, they found only a small difference between PV based and non PV based methods. Even though AIPTW and PV based methods showed significant issues with monotonicity and estimates falling out of the 0 and 1 probability bounds, they should not be disregarded since simple corrections like isotonic regression and truncation could be applied.
The authors did list several limitations of their study like using a Cox model for time-to-event processes but without time varying confounders and also using a binary treatment variable. In general though they showed that these methods outperformed the Kaplan-Meier estimator when analyzing observational data. They recommended the AIPTW based methods, since they have the doubly-robust property and had goodness-of-fit similar to IPTW based methods. They recommended R packages, riskRegression and adjustedCurves. If the EL method catches up to have its own package with the doubly robust property then it can be a viable alternative to the AIPTW based methods.
Written by,
Usha Govindarajulu
Keywords: survival, causal inference, adjusted survival, Cox model, IPTW, G-Formula
References
Denz R, Klassen-Mielke, Timmesfeld, N (2023). “A comparison of different methods to adjust survival curves for confounders”. Statistics in Medicine. https://onlinelibrary.wiley.com/doi/10.1002/sim.9681
https://onlinelibrary.wiley.com/cms/asset/b21c8b70-c759-49c0-b7e5-c8d713129b7d/sim9681-fig-0001-m.jpg