January 1, 2024
The authors were interested in the average treatment effect (ATE) which reflects how the treatment affects the potential outcome. In order to estimate ATE, propensity scores have been adapted for their estimation. such as the inverse probability weighted (IPW) or augmented IPW (AIPW) estimation methods. As they have pointed out, the key idea of the propensity score is based on the conditional probability for an individual to receive a treatment, given pre-treatment confounders. Since this estimation required precise measurements of variables but measurement error often exists, this problem would affect the ATE. In addition, in estimating the propensity score, usually parametric models are used but the authors wanted to use a model with an unknown link function, and they used machine learning methods to estimate that. The authors therefore discussed the estimation of propensity methods non-parametrically and ways to handle the measurement error in order to correct for the error. They focused on using random forests for the non-parametric estimation.
In their causal inference methods section, they discussed these issues. In the framework of causal inference, the following assumptions are required when estimating ATE: (A1) Strong ignorable treatment assumption (SITA), (A2) Stable unit treatment value assumption (SUTVA), and (A3) The positivity assumption. The A1 assumption suggested that the confounder is independent of the outcome. The A2 assumption or consistency assumption suggested that each person’s potential outcome is not reflected by others treatment assignments. Finally, the A3 assumption assures that the propensity score is between 0 and 1. They then showed their formulation of the IPW and they also discussed their estimation of the AIPW, which would have the property of being doubly robust. They also described their corrections for misclassification, which do require having external validation data, however, not everyone has access to such data so if one doesn’t have access then they suggested doing a sensitivity analysis. They then brought these corrections into their IPW or AIPW propensity scores.
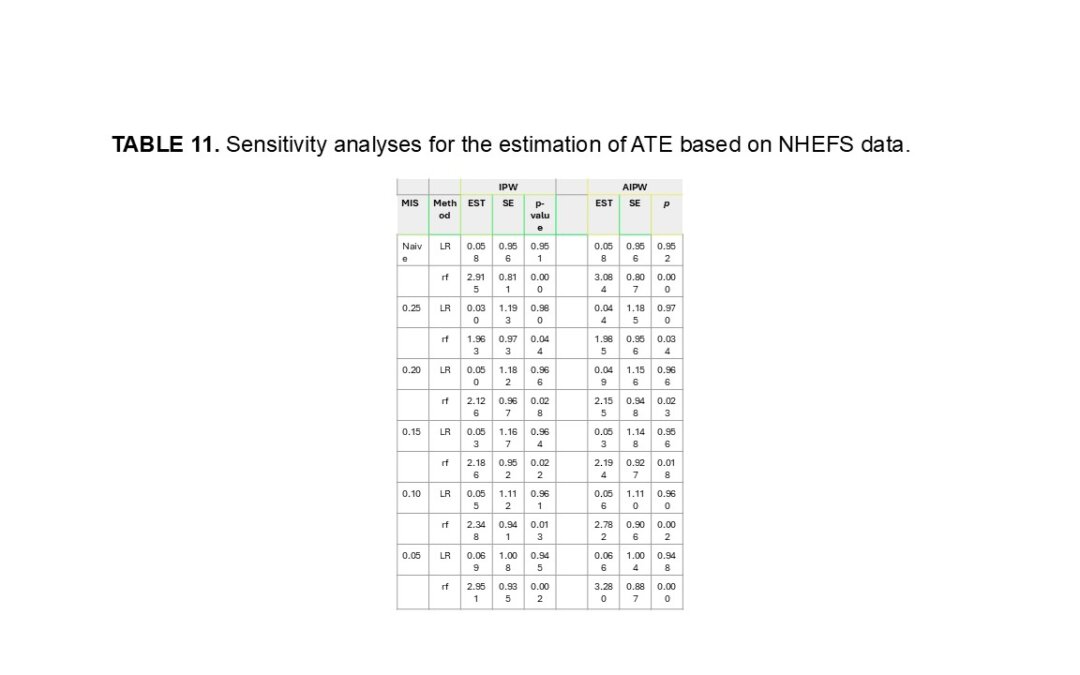
In their simulations, they discussed variable selection by the random forest method vs the lasso method, which is something they had not discussed prior in their methods section. They found the random forest method was better at not selecting unimportant variables as compared to the lasso method, which frequently selected unimportant variables even after correction for misclassification. They found that under the same “Proposed-IPW” and “Proposed-AIPW,” that the estimated ATE based on the random forest method outperforms the penalized logistic regression approach with smaller biases, SEs, and MSEs, They also showed that the random forest method was valid to handle nonlinear confounders when estimating the propensity score. They then said that given the accurate estimator of the propensity score, one can derive the precise estimator for ATE. Finally, they found that with small biases and SEs, that the Proposed-IPW and Proposed-AIPW methods determined by the random forest method have approximate 95% IC, while the IC becomes smaller if the propensity score is estimated by the penalized logistic regression model. In contrast, the IC derived by the Naive-IPW and Naive-AIPW methods is close to zero, which is unsurprising because of the tremendous biases induced by measurement error.
They were also able to confirm performance of their methods in a real data analysis using NHANES I data. In their discussion, they did admit that validation data is a requirement almost due to the need to correct misclassified data even though they had suggested sensitivity analyses could be performed. Also, they haven’t provided any code to implement this yet and that is also under work.
Written by,
Usha Govindarajulu, PhD
Keywords: survival, causal inference, average treatment effect, misclassification, propensity scores, random forest
References
Chen, L-P (2024) “Nonparametric Estimation for Propensity Scores With Misclassified Treatments”. Statistics in Medicine. https://doi.org/10.1002/sim.10306 .