November 6, 2025
For these authors, the goal of this paper was to apply pseudo-observations to estimate the regression coefficients in the Cox proportional hazards model under length-biased right-censored (LBRC) data. On some occasions as they found, observations may not be representative of the original data, and the selection of an observation is proportional to its length or duration. This is known as length-biased sampling. Length-biased data can be thought of as a special case of left-truncated data, where the truncation variable follows a uniform distribution, known as the stationarity assumption. Sampling bias may be inherent in the data as well. In addition to sampling bias, some individuals may be lost to follow-up or drop out of the study before the terminating event occurs. Therefore, in this case, they were dealing with length-biased right-censored (LBRC) data. In Equation 6 they define a G(u) but they did not describe what it represents.
In 2003, Andersen et al. had proposed a general approach to censored data regression based on pseudo-observations. The pseudo-observations were derived from jackknife theory and they also could be through standard regression methods such as the generalized estimating equations (GEE) approach (Liang and Zeger, 1986) to estimate regression coefficients. Also, this approach has been applied to various survival analysis models, including regression models for the cumulative incidence functions in competing risks. One can define the pseudo observations to be computed from the estimate of the survival function and that would be computed at the available time points.
In their study, they compared the pseudo-observation methods with two prominent standard approaches proposed by Qin and Shen (2010) and Huang and Qin (2012) for estimating the coefficients of a Cox proportional hazards model under LBRC data. Vardi (1982a) derived the nonparametric maximum likelihood estimator (NPMLE) of the survival function under LBRC data. This NPMLE does not have a closed form and would have to be obtained through implementing the expectation-maximization (EM) algorithm (Vardi 1989). There focus was on the Cox model. They then proposed a generalized linear model for the pseudo responses as survival at a fixed time point and then they estimated this regression model by GEE with a log-link function; they defined the estimating equation for this. Since the conditional survival expectation approximates the true conditional survival function then this property allowed them to use the pseudo-observations as outcome variables in the generalized linear model.
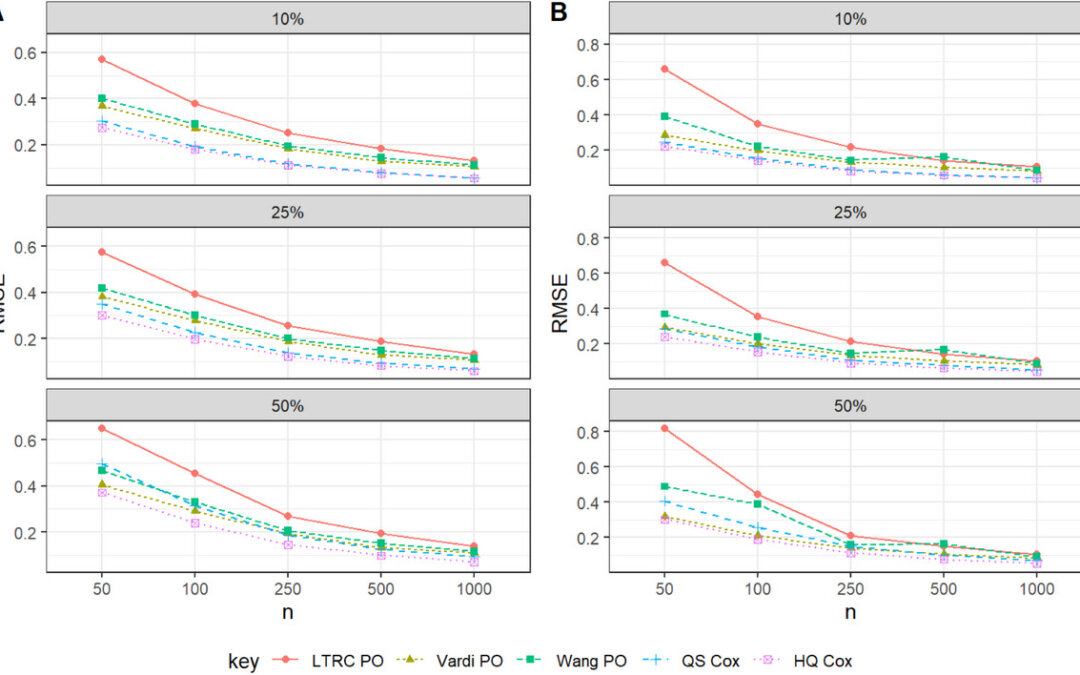
They ran simulations through Monte Carlo simulations. They compared three different pseudo-observations methods: Vardi PO, Wang PO, and LTRC PO. They also compared these to two standard estimators proposed by Qin and Shen (2010) and Huang and Qin (2012), denoted as “QS Cox” and “HQ Cox,” respectively. They found amongst the pseudo-observation (PO) methods that the Vardi PO and the Wang PO perform better in terms of RMSE compared to LTRC PO and the Vardi PO was yielding consistently lower RMSE as expected. Also across all settings, the PO methods were comparable to the likelihood-based method HQ Cox. These suggested estimation methods performed well for LRBC data in terms of the CP by approximately matching the nominal 95% confidence level. As the censoring rate increased in the different simulation settings, the bias, SE, and RMSE of the estimates also increased. Overall the PO methods did well. They plan to extend these methods to competing risks and also they would try to incorporate a non-parametric approach but they are constrained by the validity of parametric pseudo-observations which depends on assumptions like independent censoring and appropriate choice of number and positions of knots for the splines.
Written by,
Usha Govindarajulu
Keywords: survival, pseudo observations, Cox model, length bias
References:
Andersen, P. K., J. P. Klein, and S. Rosthøj. 2003. “Generalised Linear Models for Correlated Pseudo-Observations, With Applications to Multi-State Models.” Biometrika 90, no. 1: 15–27.
Akbari M, Rad NN, and Chen D-G (2025) “Pseudo-Observation Approach for Length-Biased Cox Proportional Hazards Model” Biometrical Journal. https://doi.org/10.1002/bimj.70094
Huang, C.-Y., and J. Qin. 2012. “Composite Partial Likelihood Estimation Under Length-Biased Sampling, With Application to a Prevalent Cohort Study of Dementia.” Journal of the American Statistical Association 107, no. 499: 946–957.
Qin, J., and Y. Shen. 2010. “Statistical Methods for Analyzing Right-Censored Length-Biased Data Under Cox Model.” Biometrics 66, no. 2: 382–392.
Liang, K.-Y., and S. L. Zeger. 1986. “Longitudinal Data Analysis Using Generalized Linear Models.” Biometrika 73, no. 1: 13–22.
Vardi, Y. 1982a. “Nonparametric Estimation in Renewal Processes.” The Annals of Statistics 10: 772–785.
Vardi, Y. 1989. “Multiplicative Censoring, Renewal Processes, Deconvolution and Decreasing Density: Nonparametric Estimation.” Biometrika 76, no. 4: 751–761.
https://onlinelibrary.wiley.com/cms/asset/467eedd5-5f8b-49be-b83e-a04db8e983ca/bimj70094-fig-0001-m.jpg