January 29, 2025
Many analyses have used clustered data but not everyone considers that clusters may be informative. For example, generalized estimating equations (GEE) and marginal proportional hazards model have been widely used to estimate population-average effects with clustered data, but they have not considered the impact of cluster sizes on the outcome. These cluster sizes may actually impact the outcome. Having used random effects model in generalized linear models helped to address some of this issue as well using cluster sizes as weights as inverse of the sizes in a GEE analysis. Also, consideration of testing for the informativeness of cluster sizes before including their adjustment has also been needed. This had been developed for conditional models, but it has been needed for marginal models. They addressed by developing a uniform set of test statistics encompassing score and Wald tests for GEE, the marginal proportional hazards model, and the marginal proportional sub distribution hazards model. Their method handles a wide range of outcomes (continuous, binary, categorical, survival, and competing risks outcomes) They also used weighted estimating equations to make inferences on regression parameters which represent cluster-average effects.
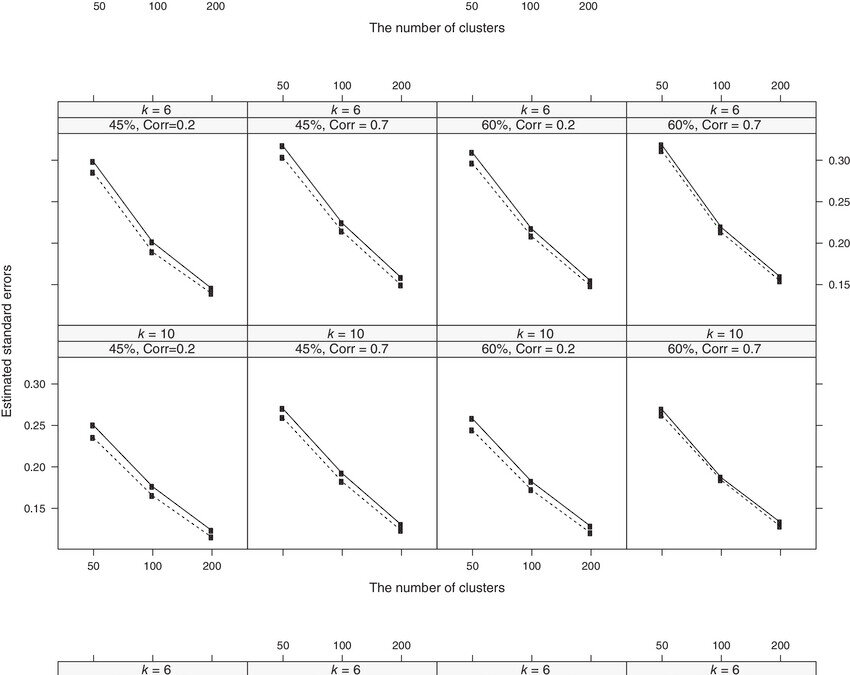
They also conducted simulations to test non-informativeness of cluster sizes for binary, survival, and competing risks outcomes. They assessed Type I error rates and power levels via Monte Carlo simulation with 1000 replicated datasets per scenario. In the first simulation study with a binary outcome, they found as cluster sizes increased than the Type I error rates became closer to 0.05 for both score and Wald tests and the power increased also. When the cluster correlation was stronger, there was more bias and worse coverage rates. They also conducted a simulation study on a count outcome with a log link function. Again they saw the same trend with Type I error rates and power as cluster sizes were increased. Also, higher cluster size led to more bias and worse coverage rates. In a third simulation study, they considered survival and competing risks outcomes. They generated clustered survival data with a positive stable frailty model. They again saw the same trends. Also, again the bias and CR worsened with increased cluster sizes.
They also conducted a real data analysis and found that cluster sizes were informative. To summarize, in their simulations they found the score test had higher power than the Wald test for the proportional hazards and sub distribution hazards model while the Wald test showed higher power than the score test for the logistic and Poisson models. This may have to do with the fact that an intercept needs to be estimated in a generalized linear model while it does not for the proportional hazards type models. They mentioned that developing methods for frailty models under survival and competing risks setting would be an important topic in the future. Also, since observational studies often suffer from missing covariates then they said the development of test statistics and statistical inference under informative cluster sizes that can handle missing data is also worthy of consideration.
In this framework they used cross-sectional data for their simulations and real data analysis but so it would be worthwhile to extend this to longitudinal data. Their test statistics can be used for longitudinal clustered data with informative sizes but they had not formally tested this. Since it is common that cluster randomized trials have small numbers of clusters than this would also be worthwhile testing.
Written by,
Usha Govindarajulu
Keywords: informative, clustering, score test, Wald test, generalized linear model, Cox model, proportional subdistrbution hazards model
References:
Kim S, Martens MJ, and Ahn KW (2024). “Test Statistics and Statistical Inference for Data With Informative Cluster Sizes” Biometrical Journal.
https://doi.org/10.1002/bimj.70021
https://onlinelibrary.wiley.com/cms/asset/b62de16b-6b61-480d-aec8-b09aefd47dc4/bimj70021-fig-0001-m.jpg